题目内容
 在边长为2的正方形ABCD中,O为对称中心,正方形OEFG绕点O旋转,边OE、OG分别与边BC、CD交于点M、N.
在边长为2的正方形ABCD中,O为对称中心,正方形OEFG绕点O旋转,边OE、OG分别与边BC、CD交于点M、N.(1)求证:OM=ON;
(2)探究四边形OMCN的面积是否随M、N的位置的变化而变化,说明理由;
(3)连结MN,探究在旋转正方形OEFG的过程中,△OMN的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
分析:(1)根据正方形的性质可得∠OAM=∠OBN=45°,OA=OB,再根据同角的余角相等可得∠AOM=∠BON,然后利用“角边角”证明△AOM和△BON全等,根据全等三角形对应边相等即可得证;
(2)由(1)知道△OBM与△OCN的面积相等,故四边形OMCN的面积=
正方形ABCD的面积=1,故可以得到四边形OMCN的面积不变,为1;
(3)当OM⊥BC时,OM和ON存在最小值,此时OM=ON=1,然后利用勾股定理求得MN的长,从而可以确定△OMN的周长的最小值;
(2)由(1)知道△OBM与△OCN的面积相等,故四边形OMCN的面积=
| 1 |
| 4 |
(3)当OM⊥BC时,OM和ON存在最小值,此时OM=ON=1,然后利用勾股定理求得MN的长,从而可以确定△OMN的周长的最小值;
解答: 解:(1)证明:在正方形ABCD中,∠OBM=∠OCN=45°,OC=OB,
解:(1)证明:在正方形ABCD中,∠OBM=∠OCN=45°,OC=OB,
∵∠BOM+∠MOC=∠BOC=90°,
∠CON+∠MOC=∠EOG=90°,
∴∠BOM=∠CON,
∵在△BOM和△CON中,
,
∴△BOM≌△CON(ASA),
∴OM=ON;
(2)不变;
理由:由(1)知道△OBM与△OCN的面积相等,故四边形OMCN的面积=
正方形ABCD的面积=1;
(3)当OM⊥BC时,OM和ON存在最小值,
此时OM=ON=1,
由勾股定理得:NM=
=
,
∴△OMN的周长存在最小值2+
;
 解:(1)证明:在正方形ABCD中,∠OBM=∠OCN=45°,OC=OB,
解:(1)证明:在正方形ABCD中,∠OBM=∠OCN=45°,OC=OB,∵∠BOM+∠MOC=∠BOC=90°,
∠CON+∠MOC=∠EOG=90°,
∴∠BOM=∠CON,
∵在△BOM和△CON中,
|
∴△BOM≌△CON(ASA),
∴OM=ON;
(2)不变;
理由:由(1)知道△OBM与△OCN的面积相等,故四边形OMCN的面积=
| 1 |
| 4 |
(3)当OM⊥BC时,OM和ON存在最小值,
此时OM=ON=1,
由勾股定理得:NM=
| OM2+ON2 |
| 2 |
∴△OMN的周长存在最小值2+
| 2 |
点评:本题考查了旋转的性质,解决此类问题的关键是正确的利用旋转不变量.正确作出辅助线是关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
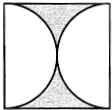 如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?
如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?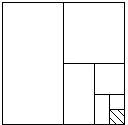 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.