题目内容
2. 如图所示,二次函数y=ax2+bx+c的图象中,某同学观察得出下面四个信息:(1)b2-4ac>0;(2)c>1;(3)2a+b<0;(4)a+b+c<0,其中正确的有( )
如图所示,二次函数y=ax2+bx+c的图象中,某同学观察得出下面四个信息:(1)b2-4ac>0;(2)c>1;(3)2a+b<0;(4)a+b+c<0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与1的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:(1)根据图示知,该函数图象与x轴有两个交点,
∴△=b2-4ac>0;
故本选项正确;
(2)由图象知,该函数图象与y轴的交点在点(0,1)上,
∴c=1;故本选项错误;
(3)由图示,知
对称轴x=-$\frac{b}{2a}$<0;
又函数图象的开口方向向下,
∴a<0,
∴b<0,即2a+b<0,
故本选项正确;
(4)根据图示可知,当x=1,即y=a+b+c<0,
∴a+b+c<0;
故本选项正确;
综上所述,其中正确的有3个;
故选:C.
点评 此题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
13.下列欧洲足球俱乐部标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列命题中,假命题是( )
| A. | 长度相等的弧是等弧 | |
| B. | 等弧必须是同圆或等圆中的弧,否则不能互相重合 | |
| C. | 度数相等的弧不一定是等弧 | |
| D. | 等弧的度数相等 |
14.下列计算正确的是( )
| A. | a•a2=a2 | B. | (a2)2=a4 | C. | 3a+2a=5a2 | D. | (a2b)3=a2•b3 |
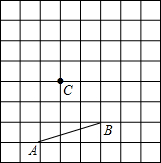 在如图所示方格纸中,按下述要求画图并回答:
在如图所示方格纸中,按下述要求画图并回答:
 已知数a、b的对应点在数轴上的位置如图所示,则a-3<b-3.
已知数a、b的对应点在数轴上的位置如图所示,则a-3<b-3.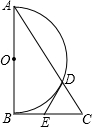 如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.