题目内容
如图,已知△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE.连接BD交AE于M,连接CE交AB于N,BD与CE交点为F,连接AF.
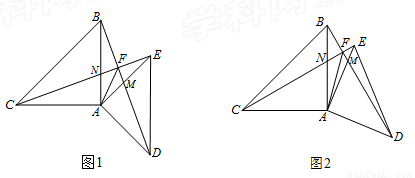
(1)如图1,求证:BD⊥CE;
(2)如图1,求证:FA是∠CFD的平分线;
(3)如图2,当AC=2,∠BCE=15°时,求CF的长.
(1)证明见试题解析;(2)证明见试题解析;(3)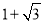 .
.
【解析】
试题分析:(1)证明△CAE≌△BAD即可;
(2)作AG⊥CE于G,AK⊥BD于K,由△CAE ≌△BAD,可以得到∠BFN=∠NAC=90°,即可得到BD⊥CE;
(3)先求出∠ACN =30°,再由含30°角的直角三角形的性质可以求出CF的长.
试题解析:(1)如图1

∵ ∠BAC =∠DAE=90°,∠BAE=∠BAE,∴ ∠CAE=∠BAD,在△CAE和△BAD中,
 ∴ △CAE≌△BAD.∴ ∠ACF=∠ABD,∵ ∠ANC=∠BNF,∴ ∠BFN=∠NAC=90°,∴ BD⊥CE;
∴ △CAE≌△BAD.∴ ∠ACF=∠ABD,∵ ∠ANC=∠BNF,∴ ∠BFN=∠NAC=90°,∴ BD⊥CE;
(2)如图1,

作AG⊥CE于G,AK⊥BD于K,由(1)知 △CAE ≌△BAD,∴ CE = BD,S△CAE =S△BAD .∴ AG = AK,∴ 点A在∠CFD的平分线上.即 FA是∠CFD的平分线;
(3)如图2

∵ ∠BAC = 90°,AB =AC,∴ ∠ACB=∠ABC =45°,∵ ∠BCE=15°,∴∠ACN =∠ACB-∠BCE= 30°=∠FBN,在Rt△ACN中,∵ ∠NAC = 90°,AC=2,∠ACN = 30°,∴AN= ,CN=
,CN= .∵ AB=AC=2,∴ BN=
.∵ AB=AC=2,∴ BN= .在Rt△ACN中,∵ ∠BFN = 90°,∠FBN = 30°,∴ NF=
.在Rt△ACN中,∵ ∠BFN = 90°,∠FBN = 30°,∴ NF=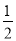 BN=
BN=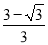 ,∴ CF=CN+NF=
,∴ CF=CN+NF=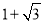 .
.
考点:1.全等三角形的判定与性质;2.含30度角的直角三角形.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案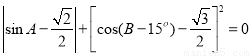 ,则△ABC是( )
,则△ABC是( ) ,使它的图象与正方形ABCD有公共点,这个函数的表达式为 .
,使它的图象与正方形ABCD有公共点,这个函数的表达式为 .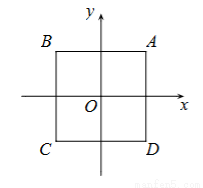

 .
.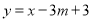 的一个交点在y轴上,求m的值.
的一个交点在y轴上,求m的值. ?
?

 b³ B.a³·a²=a
b³ B.a³·a²=a C.a
C.a ÷a²=a D.a+a=a²
÷a²=a D.a+a=a²