题目内容
如图，在平面直角坐标系中，点O为坐标系原点，矩形
OABC的边OA，OC分别在轴和轴上，其中OA=6，OC=3．已知反比例函数y=（x＞0）的图象经过BC边上的中点D，交AB于点E．
（1）k的值为 ；
（2）猜想△OCD的面积与△OBE的面积之间的关系，请说明理由．
解：∵OA=6，OC=3，点D为BC的中点，
∴D（3，3）．
∴k=3×3=9，
故答案为9；
（2）S△OCD=S△OBE，
理由是：∵点D，E在函数的图象上，
∴S△OCD=S△OAE=，
∵点D为BC的中点，
∴S△OCD=S△OBD，
即S△OBE=，
∴S△OCD=S△OBE．
练习册系列答案
名校课堂系列答案
相关题目
如图，A点的坐标为（﹣4，0），直线y=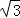
x+n与坐标轴交于点B，C，连接AC，如果∠ACD=90°，则n的值为（ ）
|
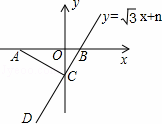
| A． | ﹣2 | B． | ﹣ | C． | ﹣ | D． | ﹣ |
解答下列问题：
如图是一个运算程序的示意图，若开始输入x的值为81，则第2014次输出的结果为（ ）
|
| A． | 3 | B． | 27 | C． | 9 | D． | 1 |
上的一个动点，连接AP，则AP的最小值是 ．