题目内容
已知一个矩形纸片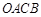 ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点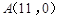 ,点
,点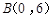 ,点
,点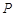 为
为 边上的动点(点
边上的动点(点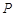 不与点
不与点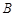 、
、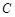 重合),经过点
重合),经过点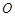 、
、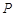 折叠该纸片,得点
折叠该纸片,得点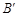 和折痕
和折痕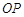 .设
.设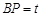 .
.
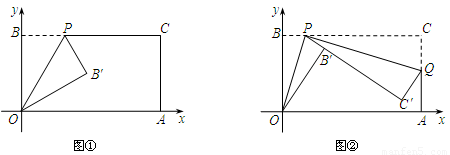
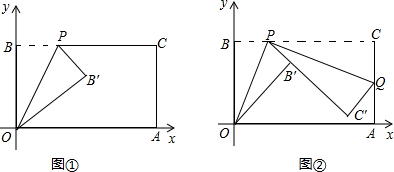
(1)如图①,当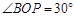 时,求点
时,求点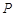 的坐标;
的坐标;
(2)如图②,经过点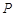 再次折叠纸片,使点
再次折叠纸片,使点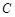 落在直线
落在直线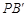 上,得点
上,得点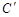 和折痕
和折痕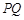 ,若
,若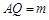 ,试用含有
,试用含有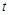 的式子表示
的式子表示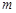 ;
;
(3)在(2)的条件下,当点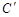 恰好落在边
恰好落在边 上时,求点
上时,求点 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
【答案】
(1)( ,6);(2)
,6);(2) ;(3)
;(3) 或
或
【解析】
试题分析:(1)根据题意 ,
, ,在
,在 中,由
中,由 ,
, ,得
,得 ,然后根据勾股定理即可列方程求解;
,然后根据勾股定理即可列方程求解;
(2)由 、
、 分别是由
分别是由 、
、 折叠得到的,可知
折叠得到的,可知 ≌
≌ ,
, ≌
≌ ,证得
,证得 ∽
∽ ,然后由相似三角形的对应边成比例,即可求得答案;
,然后由相似三角形的对应边成比例,即可求得答案;
(3)首先过点P作PE⊥OA于E,易证得△PC′E∽△C′QA,由勾股定理可求得C′A的长,然后利用相似三角形的对应边成比例与 ,即可求得t的值.
,即可求得t的值.
(1)根据题意 ,
, ,
,
在 中,由
中,由 ,
, ,得
,得 .
.
根据勾股定理, ,
,
即 ,解得
,解得 (
( 舍去)
舍去)
∴点P的坐标为( ,6);
,6);
(2)∵ 、
、 分别是由
分别是由 、
、 折叠得到的,
折叠得到的,
∴ ≌
≌ ,
, ≌
≌ .
.
∴ ,
, .
.
∵ ,
,
∴ .
.
∵ ,
,
∴ .
.
又 ,
,
∴ ∽
∽ ,有
,有 .
.
由题设 ,
, ,
, ,
, ,则
,则 ,
, .
.
∴ .
.
∴ (
( );
);
(3)点 的坐标为
的坐标为 或
或 .
.
考点:折叠的性质、矩形的性质,相似三角形的判定与性质
点评:本题知识点多,综合性强,难度较大,注意熟练掌握折叠前后图形的对应关系,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
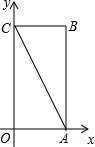 别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,
别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M, ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点 ,点
,点 ,点
,点 为
为 边上的动点(点
边上的动点(点 、
、 重合),经过点
重合),经过点 、
、 和折痕
和折痕 .设
.设 .
.
 时,求点
时,求点 上,得点
上,得点 和折痕
和折痕 ,若
,若 ,试用含有
,试用含有 的式子表示
的式子表示 ;
; 上时,求点
上时,求点