题目内容
 如图AD∥BC,∠1=∠2,∠3=∠4,直线DC过点E交AD于D,交BC于点C.求证:AD+BC=AB.
如图AD∥BC,∠1=∠2,∠3=∠4,直线DC过点E交AD于D,交BC于点C.求证:AD+BC=AB.分析:本题可采用截取法求解.在线段AB上截取AF=AD,连接EF;通过证△CBE≌△FDE,得出BF=BC,由此来证得AB=AD+BC.
解答: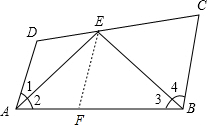 证明:在线段AB上取AF=AD,连接EF,
证明:在线段AB上取AF=AD,连接EF,
在△ADE与△AFE中,
∵
,
∴△ADE≌△AFE,
∴∠D=∠AFE,
由AD∥CB又可得∠C+∠D=180°,
∴∠AFE+∠C=180°,
又∵∠BFE+∠AFE=180°,
∴∠C=∠BFE,
在△CBE与△FBE中,
∵
,
∴△CBE≌△FBE,
∴BF=BC,
∵AB=BF+AF,
∴AB=AD+BC.
 证明:在线段AB上取AF=AD,连接EF,
证明:在线段AB上取AF=AD,连接EF,在△ADE与△AFE中,
∵
|
∴△ADE≌△AFE,
∴∠D=∠AFE,
由AD∥CB又可得∠C+∠D=180°,
∴∠AFE+∠C=180°,
又∵∠BFE+∠AFE=180°,
∴∠C=∠BFE,
在△CBE与△FBE中,
∵
|
∴△CBE≌△FBE,
∴BF=BC,
∵AB=BF+AF,
∴AB=AD+BC.
点评:本题考查了三角形全等的判定及性质;利用三角形全等是证明线段相等的重要方法,构建全等三角形的方法主要有:翻折、旋转、截取、延长等,本题采用的是截取法.

练习册系列答案
相关题目
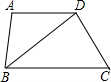 如图AD∥BC,BD平分∠ABC,若∠A=100°,则∠DBC的度数等于( )
如图AD∥BC,BD平分∠ABC,若∠A=100°,则∠DBC的度数等于( )| A、100° | B、850° | C、40° | D、50° |
 8、如图AD∥BC,那么下列结论中错误的是( )
8、如图AD∥BC,那么下列结论中错误的是( ) 如图AD∥BC,∠A+∠B=100°,∠D=70°,则∠A=
如图AD∥BC,∠A+∠B=100°,∠D=70°,则∠A=