题目内容
如图, ABCD中,
ABCD中, 为
为 中点,过点
中点,过点 作
作 的垂线交
的垂线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 .若
.若 ,
, ,
,
 ,求
,求 的长及
的长及 ABCD的周长.
ABCD的周长. 
 ABCD中,
ABCD中, 为
为 中点,过点
中点,过点 作
作 的垂线交
的垂线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 .若
.若 ,
, ,
,
 ,求
,求 的长及
的长及 ABCD的周长.
ABCD的周长. 
3,30
试题分析:根据平行四边形的性质可得
 ,
, ∥
∥ ,
, ,证得△
,证得△ 为等腰直角三角形,即可求得
为等腰直角三角形,即可求得 ,由
,由 为
为 中点可求的
中点可求的 ,再证得△
,再证得△ ≌△
≌△ ,即可求得
,即可求得 ,再根据勾股定理求得CH的长,即可求得结果.
,再根据勾股定理求得CH的长,即可求得结果.∵四边形
 是平行四边形,
是平行四边形,∴
 ,
, ∥
∥ ,
, .
.∵HG⊥
 于点
于点 ,
,∴
 .
.在△
 中,
中, ,
, ,
, ,
,∴
 .
.∵
 为
为 中点,
中点, ,
,∴
 .
.∵
 ,
,∴△
 ≌△
≌△ .
.∴
 .
.在△
 中,
中, ,
, ,
, ,
,∴
 .
.∴
 .
. ∴
 .
.∴

 的周长为30.
的周长为30.点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
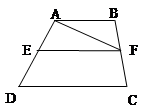
 倍,则这个多边形的边数是
倍,则这个多边形的边数是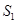 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
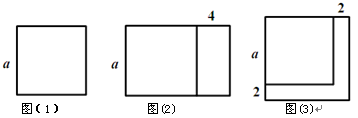


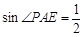 ③HP//AE ④HF=1 ⑤
③HP//AE ④HF=1 ⑤


 ,则AF的长为__________.
,则AF的长为__________.