题目内容
11. 如图,已知△ABC≌△ADC,∠BAC=60°,∠ACD=25°,那么∠D=95°.
如图,已知△ABC≌△ADC,∠BAC=60°,∠ACD=25°,那么∠D=95°.
分析 先根据全等三角形的性质得∠DAC=∠BAC=60°,然后根据三角形内角和求∠D的度数.
解答 解:∵△ABC≌△ADC,
∴∠DAC=∠BAC=60°,
∵∠DAC+∠ACD+∠D=180°,
∴∠D=180°-25°-60°=95°.
故答案为95°.
点评 本题考查了全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
1. 如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
 如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )| A. | 20° | B. | 22° | C. | 24° | D. | 26° |
2.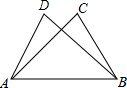 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
20.若|a|=|-4|,则a的值是( )
| A. | 4 | B. | ±4 | C. | -4 | D. | -8 |
 如图,一个加油站恰好位于两条公路m,n所夹角的平分线上,若加油站到公路m的距离是80m,则它到公路n的距离是80m.
如图,一个加油站恰好位于两条公路m,n所夹角的平分线上,若加油站到公路m的距离是80m,则它到公路n的距离是80m. 如图所示的几何体是由4个面围成,面与面相交成6条线.
如图所示的几何体是由4个面围成,面与面相交成6条线.