Question

如图，在直角三角形纸片ABC中，∠ACB=90°，∠B=30°，将纸片折叠，使AC落在斜边AB上，落点为E，折痕为AD．连接CE交AD于点F，若AF=2cm，则BD=______cm．

Answer 1

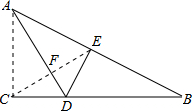
由对称可得∠AFC=90°，∠CAF=30°，
由勾股定理可得AC=AF×cos30°=

4 3

3

，
CD=AC×tan30°=

4

3

，
∵CB=AC×tan60°=4．
∴BD=BC-CD=4-

4

3

=

8

3

（cm）．
故答案为

8

3

．