题目内容
已知△ABC∽△A′B′C′，∠A=60°，∠B=75°，则∠C′为________．
45°
分析：根据△ABC∽△A′B′C′，即可求得∠C=∠C′，根据三角形内角和性质即可解题．
解答：在△ABC中，∠A=60°，∠B=75°，
∴∠C=45°，
∵△ABC∽△A′B′C′，
∴∠C=∠C′，
∴∠C′=∠C=45°．
故答案为：45°．
点评：本题考查了三角形内角和性质，相似三角形对应角相等的性质，本题中求∠C是解题的关键．
分析：根据△ABC∽△A′B′C′，即可求得∠C=∠C′，根据三角形内角和性质即可解题．
解答：在△ABC中，∠A=60°，∠B=75°，
∴∠C=45°，
∵△ABC∽△A′B′C′，
∴∠C=∠C′，
∴∠C′=∠C=45°．
故答案为：45°．
点评：本题考查了三角形内角和性质，相似三角形对应角相等的性质，本题中求∠C是解题的关键．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0，则这个三角形的形状是（ ）
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
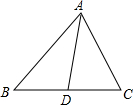如图，已知ABC中，AD为BC边上的中线，且AB=4cm，AC=3cm，则AD的取值范围是（ ）| A、3＜AD＜4 | ||||
| B、1＜AD＜7 | ||||
C、
| ||||
D、
|
已知△ABC中，cosA=
，tgB=1，则△ABC的形状是（ ）
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
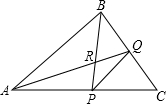如图，已知△ABC，∠B的平分线交边AC于P，∠A的平分线交边BC于Q，如果过点P、Q、C的圆也过△ABC的内心R，且PQ=1，则PR的长等于