题目内容
【题目】如图,平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() ,边
,边![]() 落在
落在![]() 正半轴上,
正半轴上,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 分别作
分别作![]() ,
,![]() 交平行四边形各边如图.若反比例函数
交平行四边形各边如图.若反比例函数![]() 的图象经过点
的图象经过点![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为__.
的值为__.

【答案】![]()
【解析】
过C作CM⊥x轴于点M,由平行四边形DCOE的面积可求得OE,过D作DN⊥x轴于点N,由C点坐标则可求得ON的长,从而可求得D点坐标,代入反比例函数解析式可求得k的值
如图,过C作CM⊥x轴于点M,过D作DN⊥x轴于点N,则四边形CMND为矩形,
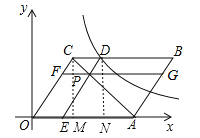
∵四边形OABC为平行四边形,
∴CD∥OE,且DE∥OC,
∴四边形DCOE为平行四边形,
∵C(2,5),
∴OM=2,CM=5,
由图可得,S△AOC=S△ABC=![]() SABCO,
SABCO,
又∵S△FCP=S△DCP且S△AEP=S△AGP,
∴SOEPF=SBGPD,
∵四边形BCFG的面积为10,
∴SCDEO=SBCFG=10,
∴S四边形DCOE=OECM=10,即5OE=10,解得OE=2,
∴CD=MN=2,
∴ON=OM+MN=2+2=4,DN=CM=5,
∴D(4,5),
∵反比例函数y=![]() 图象过点D,
图象过点D,
∴k=4×5=20.
故答案为:20.

练习册系列答案
相关题目




