题目内容
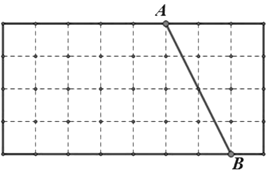
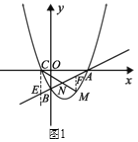
【题目】如图![]() 所示,在平面直角坐标系
所示,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一交点为点
轴的另一交点为点![]() .
.
(1)求抛物线的函数表达式;
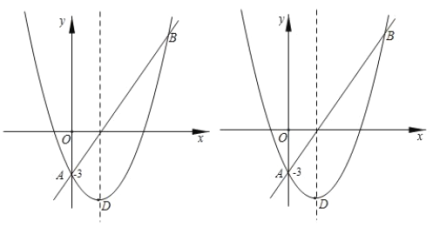
(2)点![]() 为直线
为直线![]() 下方抛物线上一动点.
下方抛物线上一动点.
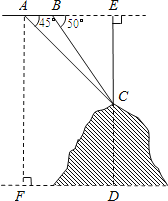
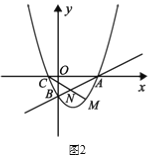
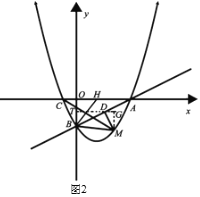
①如图2所示,直线![]() 交线段
交线段![]() 于点
于点![]() ,求
,求![]() 的最小值;
的最小值;
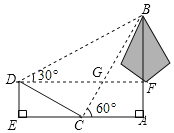
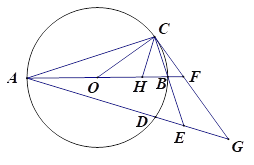
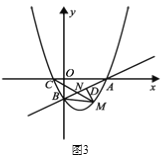
② 如图3所示,连接![]() 过点
过点![]() 作
作![]() 于
于![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,求点
的2倍?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①当
;(2)①当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;②存在,点M的坐标为
;②存在,点M的坐标为![]() 或(4,-6).
或(4,-6).
【解析】
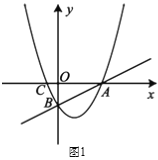
(1)解:在直线![]() ,分别令
,分别令![]() ,
,![]() .可得A(8,0)、B(0,
.可得A(8,0)、B(0,![]() 4),将A(8,0)、B(0,
4),将A(8,0)、B(0,![]() 4)代入
4)代入![]() ,解得b、c的值再代入即可解答.
,解得b、c的值再代入即可解答.
(2)解:①如图1,过C作![]() ∥
∥![]() 轴交直线AB于点E,过M作
轴交直线AB于点E,过M作![]() ∥
∥![]() 轴交直线AB于点F.可得CE∥MF,求出直线AB的解析式,进而求出C,E的坐标,即可求出答案;
轴交直线AB于点F.可得CE∥MF,求出直线AB的解析式,进而求出C,E的坐标,即可求出答案;
②由△BOC∽△ABC∠ABC=∠AOB=90°,又![]() 于
于![]() ,即∠BDM=∠ABC=90°,∠BAC < 45°.因此在
,即∠BDM=∠ABC=90°,∠BAC < 45°.因此在![]() 只能是∠BMD=2∠BAC或∠MBD=2∠BAC.在图2中,取AC中点H,连接BH,可得∠BHO=2∠BAC,
只能是∠BMD=2∠BAC或∠MBD=2∠BAC.在图2中,取AC中点H,连接BH,可得∠BHO=2∠BAC,![]() ,过D作DT
,过D作DT![]()
![]() 轴于T,过M作MG
轴于T,过M作MG![]() TD交其延长线于G.可证△TBD∽△GDM,再根据三角函数得出当∠BMD=2∠BAC时,
TD交其延长线于G.可证△TBD∽△GDM,再根据三角函数得出当∠BMD=2∠BAC时,![]() ,∠MBD=2∠BAC时,
,∠MBD=2∠BAC时,![]() ,设
,设![]() (
(![]() ),则
),则![]() ,
,![]() ,当∠BMD=2∠BAC时,
,当∠BMD=2∠BAC时,![]() ,又
,又![]() ,即可得出
,即可得出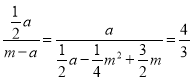 ,当∠MBD=2∠BAC时,
,当∠MBD=2∠BAC时,![]()
![]() ,
,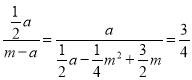 ,即可求出M的坐标
,即可求出M的坐标
(1)解:在直线![]() ,分别令
,分别令![]() ,
,![]() .可得A(8,0)、B(0,
.可得A(8,0)、B(0,![]() 4),
4),
将A(8,0)、B(0,![]() 4)代入
4)代入![]() 有
有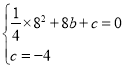
解得: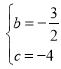
∴![]()
(2)解:①如图1,过C作![]() ∥
∥![]() 轴交直线AB于点E,过M作
轴交直线AB于点E,过M作![]() ∥
∥![]() 轴交直线AB于点F.可得CE∥MF,
轴交直线AB于点F.可得CE∥MF,
∴![]()
设![]() ,
,
∵MF∥![]() 轴交直线AB于点F,直线AB:
轴交直线AB于点F,直线AB:![]()
∴![]() ,则
,则![]()
可求得C(![]() 2,0),C作CE∥y轴交直线AB于点E,
2,0),C作CE∥y轴交直线AB于点E,
∴E(![]() 2,
2,![]() 5),CE=5.
5),CE=5.
∴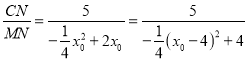 ,
,
∴当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
②存在.
理由如下:∵C(![]() 2,0);B(0,
2,0);B(0,![]() 4);A(8,0).
4);A(8,0).
∴OC=2,OB=4,OA=8
可证△BOC∽△ABC.有∠ABC=∠AOB=90°,又![]() 于
于![]()
∴∠BDM=∠ABC=90°,∠BAC < 45°.因此在![]() 只能是∠BMD=2∠BAC或∠MBD=2∠BAC.在图2中,取AC中点H,连接BH,可得∠BHO=2∠BAC,
只能是∠BMD=2∠BAC或∠MBD=2∠BAC.在图2中,取AC中点H,连接BH,可得∠BHO=2∠BAC,
OH=OA![]() AH=3,tan∠BHO=
AH=3,tan∠BHO=![]() .
.
过D作DT![]()
![]() 轴于T,过M作MG
轴于T,过M作MG![]() TD交其延长线于G.
TD交其延长线于G.
可证△TBD∽△GDM,![]()
又DM![]() AB, tan∠DMB=
AB, tan∠DMB=![]() ,tan∠DBM=
,tan∠DBM=![]() .
.
当∠BMD=2∠BAC时,∴![]() ,
,
∠MBD=2∠BAC时,![]() ,
,
设![]() (
(![]() ),
),
则![]() ,
,![]()
![]()
∴![]()
当∠BMD=2∠BAC时,![]() ,又
,又![]() ,
,
∴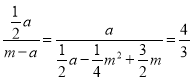
解之得![]() ,
,![]() ,又0 < m < 8,
,又0 < m < 8,
∴![]() ,点M的坐标为
,点M的坐标为![]() .
.
当∠MBD=2∠BAC时,![]()
又![]() ,
,
∴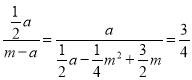
解之得![]() ,
,![]() ,又0<m<8,
,又0<m<8,
∴![]() ,点M的坐标为
,点M的坐标为![]()
综合得存在满足条件的点M的坐标为![]() 或(4,-6)
或(4,-6)