Question

如图，AC=AD，AB平分∠CAD，则图中有（　　）对全等三角形．

A．2

B．3

C．4

D．5

Answer 1

分析：根据AB平分∠CAD可得∠1=∠2，利用SAS定理可证明△ABC≌△ABD；△ACE≌△ADE，进而可证明△CEB≌△DEB．

解答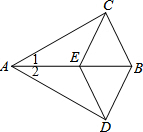：解：∵AB平分∠CAD，
∴∠1=∠2，
在△ABC和△ABD中

AC=AD ∠1=∠2 AB=AB

，
∴△ABC≌△ABD（SAS），
∴CB=BD，
在△ACE和△ADE中

AC=AD ∠1=∠2 AE=AE

，
∴△ACE≌△ADE（SAS），
∴EC=DE，
在△ECB和△EDB中

CB=DB EB=EB CE=DE

，
∴△CEB≌△DEB（SSS）．
故选：B．

点评：此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．