��Ŀ����
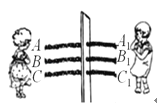
����Ŀ����ͼ������ͬ��������AA1��BB1��CC1����һ��ľ�壬�������˷ֱ�վ��ľ����������࣬ÿ�θ���ѡȡ�����һ�����ӣ�ÿ�����ӱ�ѡ�еĻ�����ȣ�
��1���ʣ�����������ͬʱѡ��ͬһ����������һ�¼��� �����¼���������������
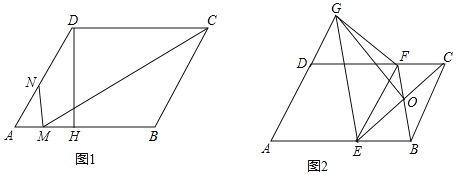
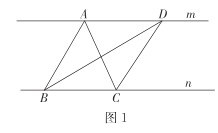
��2���ڻ�������������£�����Ƚ����A��C�������˴��һ�����ᣬ�����ô��Ҳ�A1��B1��C1�������������ѡ������һ���ᣨ�����������ɵ�ͨ��ľ�ף�������������鶯����B���ܳ�����������������һ���������ĸ����Ƕ��٣�
���𰸡���1�������![]() ����2���ܳ�����������������һ�������ĸ����ǣ�
����2���ܳ�����������������һ�������ĸ����ǣ�![]() ��
��
��������
��1����������¼��Ķ��塢�оٷ�����ʼ��ɵó��𰸣�
��2�������оٷ��г����п��ܵĽ����������ʼ���.
��1����������ͬʱѡ��ͬһ������������п��ܳ��֣�Ҳ�п��ܲ����֣���������ԣ���������¼��Ķ��壬������һ�¼�������¼���
��������ѡȡ���ӵ����п��ܽ����9�֣���![]() ������ÿһ�ֳ��ֵĿ��������
������ÿһ�ֳ��ֵĿ��������
��������ͬʱѡ��ͬһ��������3�ֿ��ܣ���![]()
�������ĸ���Ϊ��![]() ��
��
��2���������о����п��ܵĽ����3�֣�![]() ������ÿһ�ֳ��ֵĿ��������
������ÿһ�ֳ��ֵĿ��������
���鶯����B���ܳ�����������������һ�������Ľ����2�֣���![]()
�������ĸ���Ϊ��![]() .
.

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�