题目内容
一抛物线过(1,-2),(-1,2),(3,2).(1)求这条抛物线的解析式;
(2)用配方法把函数解析式化为顶点式,并写出顶点坐标;
(3)求该顶点与抛物线和x轴两交点围成的三角形面积S.
分析:(1)已知了抛物线上三点的坐标,可用待定系数法求出抛物线的解析式.
(2)依题意将(1)的抛物线解析式化为顶点式即可得出相应的结论.
(3)先根据抛物线的解析式求出抛物线与x轴的交点坐标,进而可求出两交点的距离,然后根据顶点的纵坐标的绝对值即可求出S的值.
(2)依题意将(1)的抛物线解析式化为顶点式即可得出相应的结论.
(3)先根据抛物线的解析式求出抛物线与x轴的交点坐标,进而可求出两交点的距离,然后根据顶点的纵坐标的绝对值即可求出S的值.
解答:解:(1)设抛物线的解析式为y=ax2+bx+c.
已知抛物线过(1,-2),(-1,2),(3,2)则有:
,
解得:
,
因此抛物线的解析式为y=x2-2x-1.
(2)根据(1)的抛物线解析式可知:y=(x-1)2-2,
因此抛物线的顶点坐标为(1,2).
(3)根据抛物线的解析式可知:抛物线与x轴的交点坐标为:(1+
,0),(1-
,0).
因此两交点的距离为2
.
∴S=
×2×2
=2
.
已知抛物线过(1,-2),(-1,2),(3,2)则有:
|
解得:
|
因此抛物线的解析式为y=x2-2x-1.
(2)根据(1)的抛物线解析式可知:y=(x-1)2-2,
因此抛物线的顶点坐标为(1,2).
(3)根据抛物线的解析式可知:抛物线与x轴的交点坐标为:(1+
| 2 |
| 2 |
因此两交点的距离为2
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查了用待定系数法求二次函数的解析式、二次函数顶点坐标的求法、图形面积的求法等知识点.

练习册系列答案
相关题目
 ,且OA⊥AB,∠COB=45°.
,且OA⊥AB,∠COB=45°. 已知一抛物线过点O(0,0),A(6,0),B(4,3),
已知一抛物线过点O(0,0),A(6,0),B(4,3),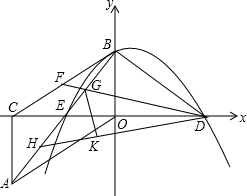 O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.
O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.