Question

【题目】在平面直角坐标系中，对于点和点，给出如下定义：

若，则称点为点的限变点．

例如：点的限变点的坐标为，点的限变点的坐标是．

（1）①的限变点的坐标是____________．

②若点在函数图象上，其限变点在函数的图象上，则函数的函数值随的增大而增大时自变量的取值范围是____________．

（2）若点在函数的图象上，其限变点的纵坐标的取值范围是，求的取值范围．

Answer 1

【答案】（1）①②或（2）

【解析】

（1）①直接根据限变点的定义得出答案即可；

②点在反比例函数图像上，点的限变点为，据此即可得解；

（2）设点的坐标为，找出当、时点的坐标，由其纵坐标的取值范围是，即可求出的取值范围．

解：（1）①∵

∴的限变点的坐标是；

②设点 的坐标为

∵当时， ，此时 随 的增大而增大；

当时， ，此时 随 的增大而增大；

当时， ，此时 随 的增大而减小；

∴综上所述，自变量的取值范围是或．

故答案是：①②或

（2）根据题意，图像上的点的限变点必在函数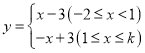的图像上，如图：

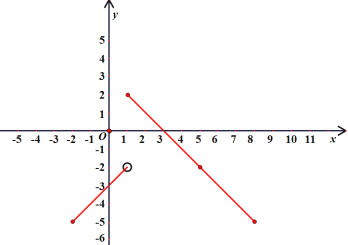
∴当，即当时，取最大值；

当时，，即；

当时，或，即或

∵

∴由图象可知，的取值范围是．

故答案是：