题目内容
△ABC中，∠C=90°，AB=8，cosA=
，则BC的长________．
2
分析：首先利用余弦函数的定义求得AC的长，然后利用勾股定理即可求得BC的长．
解答：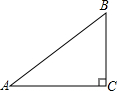
解：∵cosA=
，
∴AC=AB•cosA=8×=6，
∴BC=
=
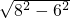=2．
故答案是：2．
点评：本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
分析：首先利用余弦函数的定义求得AC的长，然后利用勾股定理即可求得BC的长．
解答：
解：∵cosA=，∴AC=AB•cosA=8×
=6，∴BC=
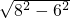==2．故答案是：2
．点评：本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，AC=2，AB=3，D是AC上一点，E是AB上一点，且∠ADE=∠B，设AD=x，AE=y，则y与x之间的函数关系式是（ ）A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
如图，在△ABC中，AB=8，AC=6，BC=7，点D在AC上，AD=2，