题目内容
如图,AB∥DE,∠ADB=90°,则∠B与∠1的关系是
- A.互余
- B.相等
- C.互补
- D.互补或相等
A
分析:根据两直线平行,内错角相等可以得到∠1=∠BAD,根据∠ADB=90°得∠B与∠BAD互余,所以∠B与∠1互余.
解答:∵AB∥DE,
∴∠1=∠BAD,
∵∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠B+∠1=90°,
∴∠B与∠1互余.
故选A.
点评:本题主要考查两直线平行,内错角相等的性质和两角互余和为90°.
分析:根据两直线平行,内错角相等可以得到∠1=∠BAD,根据∠ADB=90°得∠B与∠BAD互余,所以∠B与∠1互余.
解答:∵AB∥DE,
∴∠1=∠BAD,
∵∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠B+∠1=90°,
∴∠B与∠1互余.
故选A.
点评:本题主要考查两直线平行,内错角相等的性质和两角互余和为90°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AB∥DE,BC∥EF,则①
如图,AB∥DE,BC∥EF,则①| OA |
| OD |
| OB |
| OE |
| OC |
| OF |
| OB |
| OE |
| A、① | B、② | C、①② | D、①②③ |
 7、如图,AB∥DE,∠E=65°,则∠B+∠C=( )
7、如图,AB∥DE,∠E=65°,则∠B+∠C=( )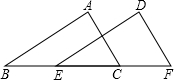 已知:如图,AB∥DE,且AB=DE.
已知:如图,AB∥DE,且AB=DE. 9、如图,AB∥DE,∠E=65°,则∠B+∠C=
9、如图,AB∥DE,∠E=65°,则∠B+∠C= 已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?
已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?