题目内容
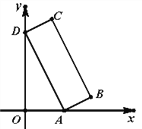
【题目】正方形ABCD中,点E是边AD的中点.连接BE,在BE上找一点F,连接AF,将AF绕点A顺时针旋转90°到AG,点F与点G对应.AG、BD延长线交于点H.若AB=4,当F、E、G三点共线时,求S△BFH=_____.

【答案】![]()
【解析】试题解析:如图所示,连接DG,过H作HP⊥BG,交BG的延长线于P,

AF绕点A顺时针旋转90°到AG,则AF=AG,∠FAG=90°,
即△AFG是等腰直角三角形,
又∵AB=AD,∠BAD=90°,
∴∠BAF=∠DAG,
∴△ABF≌△ADG,
∴BF=DG,∠AFB=∠AGD,
∵Rt△ABE中,AB=4,AE=2,
∴BE=2![]() ,
,
∵∠AFG=∠AGF=45°,
∴∠AFB=135°=∠AGD,
∴∠DGE=135°﹣45°=90°,即DG⊥BE,
∵![]() ×BE×DG=
×BE×DG=![]() ×DE×AB,
×DE×AB,
∴DG=![]() ,
,
∴Rt△BDG中,BG=![]() ,
,
∵∠HGP=∠AGF=45°,∠P=90°,
∴△GPH为等腰直角三角形,
设PH=x,则PG=x,
∵DG∥PH,
∴△BDG∽△BHP,
∴![]() ,即
,即 ,
,
解得x=![]() ,
,
∴PH=![]() ,
,
又∵BF=DG=![]() ,
,
∴S△BFH=![]() BF×PH=
BF×PH=![]() ×
×![]() ×
×![]() =
=![]() .
.
故答案为: ![]() .
.

练习册系列答案
相关题目