题目内容
 如图,在六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F.
如图,在六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F.(1)试说明△MAF为等边三角形;
(2)请探索AB,BC,EF,DE之间的关系(等量关系或位置关系)并说明理由.
分析:(1)根据多边形的内角和定理求出∠A=∠B=∠C=∠D=∠E=∠F=120°,求出∠MAF=∠MFA=60°,得出等边三角形MAF,推出MA=MF,同理求出△NBC、△MNG、△EDG是等边三角形,推出BN=BC,DE=EG,求出AN=FG,即可求出答案.
解答:解:(1)作直线AB、直线EF、直线CD,AB和EF交于M,AB和CD交于N,EF和CD交于G,
∵∠A=∠B=∠C=∠D=∠E=∠F,∠A+∠B+∠C+∠D+∠E+∠F=(6-2)×180°,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°,
∴∠MAF=∠MFA=180°-120°=60°,
∴MF=MA,
∴△MAF为等边三角形.
(2)AB+BC=EF+DE,
理由是:∵∠ABC=∠BCD=120°,
∴∠NBC=∠NCB=180°-120°=60°,
∴NB=NC,
∴△BNC是等边三角形,
∴BC=BN,∠N=60°,
同理DE=EG,∠G=60°,
∴∠G=∠N=60°,
∴MN=MG,
∵△MAF为等边三角形,
∴MA=MF,
∴MN-MA=MG-MF,
∴AN=FG,
∵AB+BC=AB+BN=AN,FG=EF+EG=EF+DE,
∴AB+BC=EF+DE.
∵∠A=∠B=∠C=∠D=∠E=∠F,∠A+∠B+∠C+∠D+∠E+∠F=(6-2)×180°,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°,
∴∠MAF=∠MFA=180°-120°=60°,
∴MF=MA,
∴△MAF为等边三角形.
(2)AB+BC=EF+DE,

理由是:∵∠ABC=∠BCD=120°,
∴∠NBC=∠NCB=180°-120°=60°,
∴NB=NC,
∴△BNC是等边三角形,
∴BC=BN,∠N=60°,
同理DE=EG,∠G=60°,
∴∠G=∠N=60°,
∴MN=MG,
∵△MAF为等边三角形,
∴MA=MF,
∴MN-MA=MG-MF,
∴AN=FG,
∵AB+BC=AB+BN=AN,FG=EF+EG=EF+DE,
∴AB+BC=EF+DE.
点评:本题考查了多边形的内角和定理,等边三角形的性质和判定的应用,注意:有一个角等于60°的等腰三角形是等边三角形.

练习册系列答案
相关题目
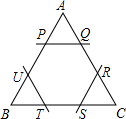 如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )
如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
 23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.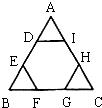 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是 如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为
如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为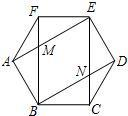 如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.