题目内容
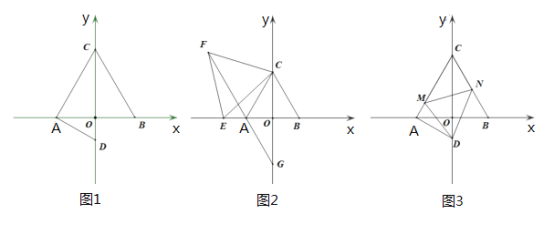
【题目】如图,等边![]() 中,
中,![]() ,
,![]() 关于
关于![]() 轴对称,
轴对称,![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,
,![]() .
.
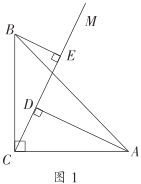
(1)如图1,求![]() 点坐标;
点坐标;
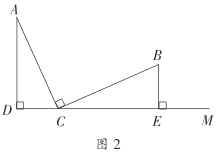
(2)如图2,![]() 为
为![]() 轴负半轴上任一点,以
轴负半轴上任一点,以![]() 为边作等边
为边作等边![]() ,
,![]() 的延长线交
的延长线交![]() 轴于点
轴于点![]() ,求
,求![]() 的长;
的长;
(3)如图3,在(1)的条件下,以![]() 为顶点作
为顶点作![]() 的角,它的两边分别与
的角,它的两边分别与![]() 、
、![]() 交于点
交于点![]() 和
和![]() ,连接
,连接![]() .探究线段
.探究线段![]() 、
、![]() 、
、![]() 之间的关系,并子以证明.
之间的关系,并子以证明.
【答案】(1)![]() ;(2)6;(3)
;(2)6;(3)![]() ,证明详见解析
,证明详见解析
【解析】
(1)先证∠ACO=30°,在Rr△ACO中由勾股定理求出AC的长,再在Rt△ACD中求出CD的长,即可求出OD的长,进步写出点D坐标;
(2)证△FCA9≌△ECB,求出∠GAO=60°,再证△CAO2△GAO,即可得到OG=OC=6;
(3)如图3,延长MA至点H,使AH=BN,连接BD,先证△DAH≌△DBN,再证△DMI≌△DMN,即可推出AM+BN=MN.
(1)(1)△ABC为等边三角形,A,B关于y轴对称,C(0,6),
∵![]()
∴![]()
在![]() 中设
中设![]() 则
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得,![]() (取正值),
(取正值),
∴![]()
∵![]()
∴在![]() 中,设
中,设![]() 则
则![]() ,
,
∵![]()
![]()
解得,![]() (取正值)
(取正值)
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)![]() 、
、![]() 均为等边三角形
均为等边三角形
![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中
中
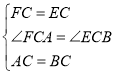
![]()
![]()
![]()
![]() ,
,![]() 平分
平分![]()
![]() .
.
(3)![]() ,证明如下:
,证明如下:
如图,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,
,
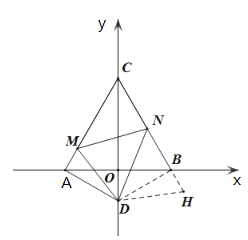
由题意得:![]() ,
,![]()
在![]() 和
和![]() 中
中
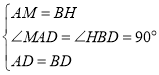
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
又![]()
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中
中

![]()
![]()
![]()
![]() .
.

练习册系列答案
相关题目