题目内容
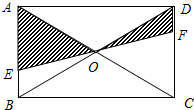 如图,矩形ABCD的面积是4,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,那么阴影部分的面积是________.
如图,矩形ABCD的面积是4,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,那么阴影部分的面积是________.
1
分析:根据矩形性质得出OB=OD,OC=OA,AB∥CD,求出△EBO≌△FDO,S矩形ABCD=2S△ABC=4S△AOB,即可求出阴影部分的面积是 S矩形ABCD,代入求出即可.
S矩形ABCD,代入求出即可.
解答: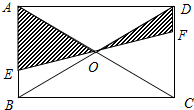 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴OB=OD,OC=OA,AB∥CD,
∴∠EBO=∠FDO,
在△EBO和△FDO中
 ,
,
∴△EBO≌△FDO(ASA),
∴S△EBO=S△FDO,
∵S矩形ABCD=AB×BC,S△ABC= ×AB×BC,S△AOB=
×AB×BC,S△AOB= S△ABC,
S△ABC,
∴S矩形ABCD=2S△ABC=4S△AOB,
∴阴影部分的面积是:S△AOE+S△DFO=S△AOE+S△BOE=S△AOB= S矩形ABCD=
S矩形ABCD= ×4=1,
×4=1,
故答案为:1.
点评:本题考查了全等三角形的性质和判定,矩形的性质,平行线的性质,三角形的面积等知识点,关键是求出阴影部分的面积=S△AOB= S矩形ABCD.
S矩形ABCD.
分析:根据矩形性质得出OB=OD,OC=OA,AB∥CD,求出△EBO≌△FDO,S矩形ABCD=2S△ABC=4S△AOB,即可求出阴影部分的面积是
 S矩形ABCD,代入求出即可.
S矩形ABCD,代入求出即可.解答:
 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,∴OB=OD,OC=OA,AB∥CD,
∴∠EBO=∠FDO,
在△EBO和△FDO中
 ,
,∴△EBO≌△FDO(ASA),
∴S△EBO=S△FDO,
∵S矩形ABCD=AB×BC,S△ABC=
 ×AB×BC,S△AOB=
×AB×BC,S△AOB= S△ABC,
S△ABC,∴S矩形ABCD=2S△ABC=4S△AOB,
∴阴影部分的面积是:S△AOE+S△DFO=S△AOE+S△BOE=S△AOB=
 S矩形ABCD=
S矩形ABCD= ×4=1,
×4=1,故答案为:1.
点评:本题考查了全等三角形的性质和判定,矩形的性质,平行线的性质,三角形的面积等知识点,关键是求出阴影部分的面积=S△AOB=
 S矩形ABCD.
S矩形ABCD. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
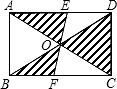 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为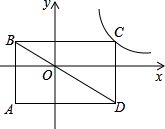 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线 (2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )
(2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( ) 如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=
如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=