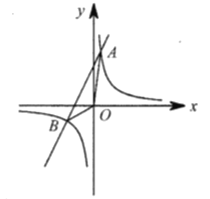
题目内容
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]()
(1)求![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)若![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() 指出点
指出点![]() 各位于哪个象限,并说明理由.
各位于哪个象限,并说明理由.
(4)点![]() 为
为![]() 轴上一个动点,若
轴上一个动点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)M在第三象限,N在第一象限;(4)E的坐标为
;(3)M在第三象限,N在第一象限;(4)E的坐标为![]() 或
或![]() .
.
【解析】
(1)先将A点代入反比例函数解析式中即可求出![]() 的值,然后根据反比例函数解析式求出B的坐标,再将A,B代入一次函数中即可求出
的值,然后根据反比例函数解析式求出B的坐标,再将A,B代入一次函数中即可求出![]() 的值;
的值;
(2)直接利用A,B点的坐标结合图象即可得出答案;
(3)根据反比例函数的图象和性质即可确定答案;
(4)设点E的坐标为![]() ,然后利用
,然后利用![]() 建立一个关于 m的方程,解方程即可.
建立一个关于 m的方程,解方程即可.
(1)∵反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]()
∴将点![]() 代入反比例函数中得
代入反比例函数中得![]() ,
,
解得![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() .
.
将![]() 代入一次函数中得
代入一次函数中得
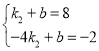 解得
解得![]()
∴![]() ;
;
(2)根据图象可知,当![]() 时,反比例函数图象在一次函数图象下方,此时
时,反比例函数图象在一次函数图象下方,此时![]() 或
或![]() ,
,
∴![]() 的解集为
的解集为![]() 或
或![]() ;
;
(3)∵反比例函数![]() 的图象在一,三象限 ,而且在每个象限内,y随着x的增大而减小,
的图象在一,三象限 ,而且在每个象限内,y随着x的增大而减小,
∵![]() ,
,
∴M,N在不同的象限,
∴M在第三象限,N在第一象限;
(4)设点E的坐标为![]() ,直线AB与x轴的交点为F,
,直线AB与x轴的交点为F,
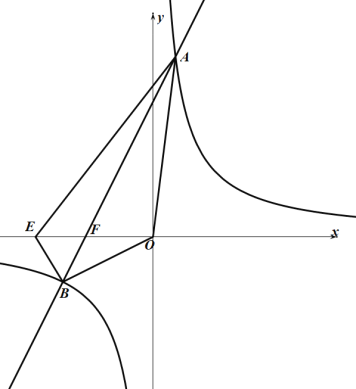
令![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() ,
,
∴E的坐标为![]() 或
或![]() .
.

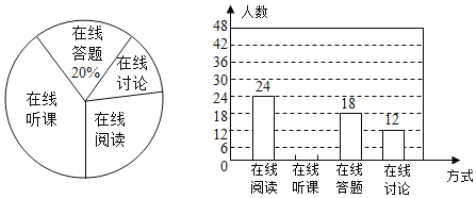
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③