题目内容
如图，在半径为13的⊙O中，0C垂直AB于点B，交⊙O于点C，AB=24，求CD的长．分析：连接OA，根据垂径定理求出AD=12，根据勾股定理求出OD，即可得出答案．
解答：解：
连接OA，
∵AB⊥CO，OC过O，
∴AD=BD=
AB=12，
在Rt△OAD中，∠ODA=90°，OA=13，AD=12，由勾股定理得：OD=5，
∴CD=13-5=8．
连接OA，
∵AB⊥CO，OC过O，
∴AD=BD=
| 1 |
| 2 |
在Rt△OAD中，∠ODA=90°，OA=13，AD=12，由勾股定理得：OD=5，
∴CD=13-5=8．
点评：本题考查了勾股定理，垂径定理的应用，关键是求出AD、OD长．
练习册系列答案
相关题目
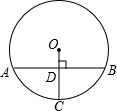（2012•湛江）如图，在半径为13的⊙O中，OC垂直弦AB于点D，交⊙O于点C，AB=24，则CD的长是
