题目内容
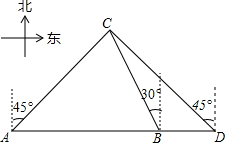 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时40海里.求A、D两点间的距离.(结果不取近似值)
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时40海里.求A、D两点间的距离.(结果不取近似值)考点:解直角三角形的应用-方向角问题
专题:
分析:先作CE⊥AD,根据BD=20,AE=DE,可求AE的长,从而求得AD的长.
解答: 解:作CE⊥AD于点E,设AE=x,则CE=AE=x,BE=
解:作CE⊥AD于点E,设AE=x,则CE=AE=x,BE=
x,
∵BD=20,AE=DE,
∴x=
x+20,
∴x=30+10
,AD=2x=60+20
;
答:A、D两点间的距离为60+20
海里.
 解:作CE⊥AD于点E,设AE=x,则CE=AE=x,BE=
解:作CE⊥AD于点E,设AE=x,则CE=AE=x,BE=
| ||
| 3 |
∵BD=20,AE=DE,
∴x=
| ||
| 3 |
∴x=30+10
| 3 |
| 3 |
答:A、D两点间的距离为60+20
| 3 |
点评:本题考查了方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,关键是作出辅助线,构造直角三角形.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 如图,AB是半圆的直径,点D是
如图,AB是半圆的直径,点D是 |
| AC |
( )
| A、100° | B、105° |
| C、110° | D、115° |
在一次函数y=(m+2)x-3中,y的值随x的值的增大而增大,则m的范围是( )
| A、m<-2 | B、m>-2 |
| C、m=-2 | D、m<2 |
 在数轴上表示下列各数,并用“<”把它们连接起来.
在数轴上表示下列各数,并用“<”把它们连接起来. 如图,已知抛物线与x轴的一个交点为A(1,0),对称轴是x=-1,则抛物线与x轴的另一个交点坐标是
如图,已知抛物线与x轴的一个交点为A(1,0),对称轴是x=-1,则抛物线与x轴的另一个交点坐标是