Question

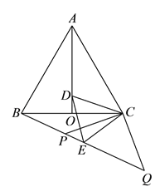
【题目】如图1，菱形纸片ABCD的边长为2，∠ABC=60°，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合于对角线BD上一点P（如图2），则六边形AEFCHG面积的最大值是（ ）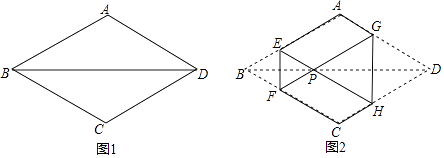
A.
B.
C.2﹣
D.1+

Answer 1

【答案】A
【解析】解：六边形AEFCHG面积=菱形ABCD的面积﹣△EBF的面积﹣△GDH的面积．

∵菱形纸片ABCD的边长为2，∠ABC=60°，

∴AC=2，

∴BD=2 ，

∴S菱形ABCD= ACBD= 2×2 =2 ，

设AE=x，

则六边形AEFCHG面积=2 ﹣ ×（2﹣x） （2﹣x）﹣ x x

=﹣ x2+ x+

=﹣ （x﹣1）2+ ，

∴六边形AEFCHG面积的最大值是 ．

故选A．

【考点精析】掌握二次函数的最值和菱形的性质是解答本题的根本，需要知道如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．