��Ŀ����
����Ŀ����ֱ����һ��![]() Ϊ�˵�������
Ϊ�˵�������![]() ��ʹ
��ʹ![]() ����һ��ֱ�����ǰ�
����һ��ֱ�����ǰ�![]() ������
������![]() ����ֱ�Ƕ�����ڵ�
����ֱ�Ƕ�����ڵ�![]() ����
����
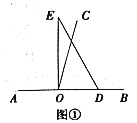
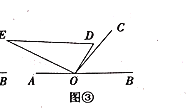
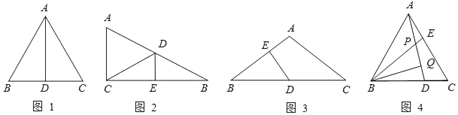
��1����ͼ�٣���ֱ�����ǰ�![]() ��һ��
��һ��![]() ��������
��������![]() �ϣ���
�ϣ���![]() ____
____![]() ��
��
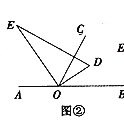
��2����ͼ������ֱ�����ǰ�![]() �Ƶ�
�Ƶ�![]() ��ʱ��ת����ij��λ�ã���
��ʱ��ת����ij��λ�ã���![]() ǡ��ƽ��
ǡ��ƽ��![]() ����
����![]() ���ڵ������Ƿ�Ϊ
���ڵ������Ƿ�Ϊ![]() ��ƽ���ߣ���˵�����ɣ�
��ƽ���ߣ���˵�����ɣ�
��3����ͼ�ۣ�����![]() �ǵ�ֱ�����ǰ�
�ǵ�ֱ�����ǰ�![]() ��ͼ�ٵ�λ�ÿ�ʼ�Ƶ�
��ͼ�ٵ�λ�ÿ�ʼ�Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ���ʱ����ת������ת��Ϊ
���ٶ���ʱ����ת������ת��Ϊ![]() ����ת��ʱ��Ϊ
����ת��ʱ��Ϊ![]() �룬����ת�������Ƿ�������ǰ��һ������
�룬����ת�������Ƿ�������ǰ��һ������![]() ��ֱ�������ڣ���ֱ��д����ʱ
��ֱ�������ڣ���ֱ��д����ʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��30����2���ǣ�֤������������3�����ڣ�![]() ��
��![]()
��������
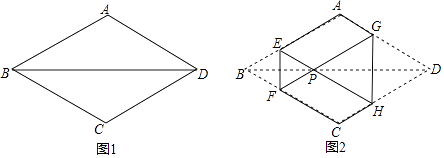
��1�������BOE=��COE+��COB������ɣ�
��2����![]() ƽ��
ƽ��![]() ���
���![]() �����ݽǵĺͲ����
�����ݽǵĺͲ����![]() ��
��![]() ���Ӷ��Ƴ���COD=��DOB�����ɵó����ۣ�
���Ӷ��Ƴ���COD=��DOB�����ɵó����ۣ�
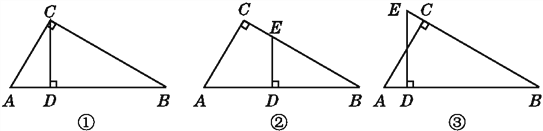
��3����DE��OC�ڵ�Mʱ��OE��OCʱ��OD��OCʱ����������ֱ��з�����⣮
�⣺��1���ߡ�BOE=��COE+��COB=90����
�֡ߡ�COB=60����
���COE=30����
�ʴ�Ϊ��30��
��2��![]() ���ڵ�������
���ڵ�������![]() ��ƽ����
��ƽ����
�������£�
![]()
![]()
![]() ƽ��
ƽ��![]()
![]()
![]()
![]()
![]()
![]() ���ڵ�����ƽ��
���ڵ�����ƽ��![]() ��
��
��3���ٵ�DE��OC�ڵ�Mʱ
�������֪��ֱ�����ǰ��С�D=60��
���ʱ��COD=30�㣬��BOD=��BOC-��COD=30��
10t=30�����t=3��
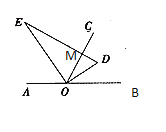
�ڵ�OE��OCʱ
��ʱ��D��OC�ϣ���BOC=60��
10t=60�����t=6��

�۵�OD��OCʱ��
��ʱ��BOD=60��+90��=150��
10t=150�����t=15
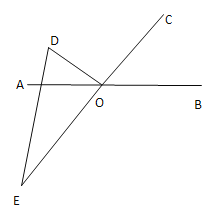
����������![]() ��
��![]() ʱ�����ǰ��һ������
ʱ�����ǰ��һ������![]() ��ֱ��
��ֱ��

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�