题目内容
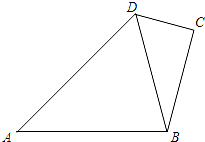 如图,已知在四边形ABCD中,∠C=90°,AB=AD=10,cos∠ABD=
如图,已知在四边形ABCD中,∠C=90°,AB=AD=10,cos∠ABD=| 2 | 5 |
分析:首先过A作AE⊥BD于E,构造直角三角形,利用等腰三角形的知识得出BE=DE=
BD,由cos∠ABD=
,得出BE的长,以及BD的长,进而运用解直角三角形知识求出BC的长.
| 1 |
| 2 |
| 2 |
| 5 |
解答: 解:过A作AE⊥BD于E,
解:过A作AE⊥BD于E,
∵AB=AD,
∴BE=DE=
BD,
在Rt△ABE中,
∵AB=10,cos∠ABD=
,
∴BE=4,
∴BD=8,
Rt△BCD中,
∵∠C=90°,BD=8,∠BDC=60°
∴BC=4
.
 解:过A作AE⊥BD于E,
解:过A作AE⊥BD于E,∵AB=AD,
∴BE=DE=
| 1 |
| 2 |
在Rt△ABE中,
∵AB=10,cos∠ABD=
| 2 |
| 5 |
∴BE=4,
∴BD=8,
Rt△BCD中,
∵∠C=90°,BD=8,∠BDC=60°
∴BC=4
| 3 |
点评:此题主要考查了解直角三角形的知识,作出垂线构造直角三角形是解决问题的关键,这种方法经常运用于解直角三角形的问题.

练习册系列答案
相关题目
 如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.
如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由. 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.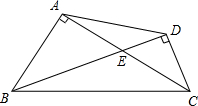 (2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.
(2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25. 如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.
如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.