题目内容
如图，ABCD是正方形，△PAB是等边三角形，则∠CPD为
- A.15°
- B.20°
- C.25°
- D.30°
D
分析：由等边三角形的性质可得∠PAB=60°，进而可得∠PAD=150°，又因为AD=AP，结合等腰三角形的性质，易得∠APD的大小；同理可以求得∠CPB的大小；最后根据图形可以求得∠CPD的度数．
解答：
解：△PAB是等边三角形；
∴∠APB=∠PAB=60°；
又∵ABCD是正方形，
∴∠BAD=90°，
∴∠PAD=∠PAB+∠BAD=90°+60°=150°，
又由AB=AP=AD，
∴AP=AD，
故∠APD=
（180°-150°）=15°；
同理求得∠BPC=15°，
∴∠CPD=∠APB-∠APD-∠BPC=30°；
故选D．
点评：本题主要考查了正方形、等边三角形的性质．正方形基本性质：①两组对边分别平行；四条边都相等；相邻边互相垂直；②四个角都是90°．
分析：由等边三角形的性质可得∠PAB=60°，进而可得∠PAD=150°，又因为AD=AP，结合等腰三角形的性质，易得∠APD的大小；同理可以求得∠CPB的大小；最后根据图形可以求得∠CPD的度数．
解答：
解：△PAB是等边三角形；∴∠APB=∠PAB=60°；
又∵ABCD是正方形，
∴∠BAD=90°，
∴∠PAD=∠PAB+∠BAD=90°+60°=150°，
又由AB=AP=AD，
∴AP=AD，
故∠APD=
（180°-150°）=15°；同理求得∠BPC=15°，
∴∠CPD=∠APB-∠APD-∠BPC=30°；
故选D．
点评：本题主要考查了正方形、等边三角形的性质．正方形基本性质：①两组对边分别平行；四条边都相等；相邻边互相垂直；②四个角都是90°．
练习册系列答案
相关题目
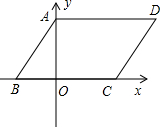x2-7x+12=0的两个根，且OA＞OB．
