题目内容
3.如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”.例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”,再加22,545,3883,345543,…,都是“和谐数”.(1)请你直接写出3个四位“和谐数”;请你猜想任意一个四位“和谐数”能否被11整除?并说明理由;
(2)已知一个能被11整除的三位“和谐数”,设其个位上的数字x(1≤x≤4,x为自然数),十位上的数字为y,求y与x的函数关系式.
分析 (1)根据“和谐数”的定义(把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同)写出四个“和谐数”,设任意四位“和谐数”形式为:$\overline{abcd}$,根据和谐数的定义得到a=d,b=c,则 $\frac{\overline{abcd}}{11}$=$\frac{1000a+100b+10c+d}{11}$=$\frac{1000a+100b+10b+a}{11}$=91a+10b为正整数,易证得任意四位“和谐数”都可以被11整除;
(2)设能被11整除的三位“和谐数”为:$\overline{xyz}$,则$\frac{\overline{xyz}}{11}$=$\frac{101x+10y}{11}$=$\frac{99x+11y+2x-y}{11}$=9x+y+$\frac{2x-y}{11}$为正整数.故y=2x(1≤x≤4,x为自然数).
解答 解:(1)四位“和谐数”:1221,1331,1111,6666…(答案不唯一)
任意一个四位“和谐数”都能被11整除,理由如下:
设任意四位“和谐数”形式为:$\overline{abcd}$,则满足:
最高位到个位排列:a,b,c,d.
个位到最高位排列:d,c,b,a.
由题意,可得两组数据相同,则:a=d,b=c,
则 $\frac{\overline{abcd}}{11}$=$\frac{1000a+100b+10c+d}{11}$=$\frac{1000a+100b+10b+a}{11}$=91a+10b为正整数.
∴四位“和谐数”能被11整数,
又∵a,b,c,d为任意自然数,
∴任意四位“和谐数”都可以被11整除;
(2)设能被11整除的三位“和谐数”为:$\overline{xyz}$,则满足:
个位到最高位排列:x,y,z.
最高位到个位排列:z,y,x.
由题意,两组数据相同,则:x=z,
故 $\overline{xyz}$=$\overline{xyx}$=101x+10y,
故$\frac{\overline{xyz}}{11}$=$\frac{101x+10y}{11}$=$\frac{99x+11y+2x-y}{11}$=9x+y+$\frac{2x-y}{11}$为正整数.
故y=2x(1≤x≤4,x为自然数).
点评 本题考查了因式分解的应用.解题的关键是弄清楚“和谐数”的定义,从而写出符合题意的数.

| A. | a0=1 | B. | a-1=-a | C. | (-a)2=-a2 | D. | a${\;}^{\frac{1}{2}}$=$\frac{1}{{a}^{2}}$ |
| A. | 220 | B. | 218 | C. | 216 | D. | 209 |
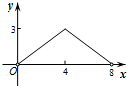
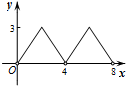
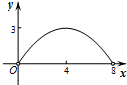
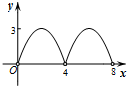
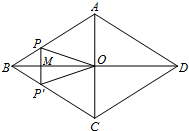 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )