题目内容
 如图,点C、F在BE上,∠A=∠D,AB∥DE,AC=DF.试说明:
如图,点C、F在BE上,∠A=∠D,AB∥DE,AC=DF.试说明:(1)△ABC≌△DEF;
(2)BF=EC.
分析:(1)首先根据平行线的性质可得∠B=∠E,再加上条件∠A=∠D,AC=DF可利用AAS定理判定△ABC≌△DEF;
(2)根据全等三角形的性质可得BC=EF,再同时加上CF即可得到结论.
(2)根据全等三角形的性质可得BC=EF,再同时加上CF即可得到结论.
解答:证明:(1)∵AB∥DE,
∴∠B=∠E,
在△ABC和△DEF中
,
∴△ABC≌△DEF(AAS);
(2)∵△ABC≌△DEF,
∴CB=EF,
∴BC+CF=EF+CF,
即FB=EC.
∴∠B=∠E,
在△ABC和△DEF中
|
∴△ABC≌△DEF(AAS);
(2)∵△ABC≌△DEF,
∴CB=EF,
∴BC+CF=EF+CF,
即FB=EC.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 21、已知:如图,点C、D在BE上,BC=DE,AB∥EF,AD∥CF.求证:AD=CF.
21、已知:如图,点C、D在BE上,BC=DE,AB∥EF,AD∥CF.求证:AD=CF. 10、如图,点C、F在BE上,∠1=∠2,BC=EF.请补充条件:
10、如图,点C、F在BE上,∠1=∠2,BC=EF.请补充条件: (2013•广东模拟)已知:如图,点C、D在BE上,BC=DE,AB∥EF,AD∥CF,AF与CD相交于O
(2013•广东模拟)已知:如图,点C、D在BE上,BC=DE,AB∥EF,AD∥CF,AF与CD相交于O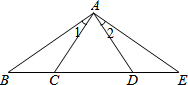 如图,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个边或角的条件,你添加的条件是
如图,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个边或角的条件,你添加的条件是