Question

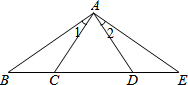如图，点C、D在BE上，BC=DE，∠1=∠2，要使得△ABD≌△AEC，还需要添加一个边或角的条件，你添加的条件是

∠B=∠E

．

Answer 1

分析：添加∠B=∠E，由条件BC=DE可得BD=CE，由∠1=∠2可得∠BAD=∠EAC，然后可利用AAS定理证明△ABD≌△AEC．

解答：解：添加∠B=∠E；
∵BC=DE，
∴CB+CD=DE+CD，
即BD=CE，
∵∠1=∠2，
∴∠1+∠CAD=∠2+∠CAD，
即∠BAD=∠EAC，
在△ABD和△AEC中，

∠B=∠E ∠BAD=∠EAC DB=CE

，
∴△ABD≌△AEC（AAS），
故答案为：∠B=∠E．

点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．