题目内容
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4.(1)求证:△ABE∽△ABD;
(2)求tan∠ADB的值;
(3)延长BC至F,连接FD,使△BDF的面积等于
 ,求∠EDF的度数.
,求∠EDF的度数.
【答案】分析:(1)由于A是弧BC的中点,故∠ADB=∠ABC,再加上公共角∠A,即可证得所求的三角形相似.
(2)由(1)的相似三角形所得比例线段,可求得AB的长,进而可在Rt△ABD中,求得∠ABD的正切值.
(3)连接CD,由(2)知∠ADB=30°,那么∠CDE=30°,∠CED=60°,由DE的长即可得到CD的值,进而可由△BDF的面积求得BF的长,进而可求得EF=ED=4,由此可证得△EDF是正三角形,即可得∠EDF的度数.
解答:(1)证明:∵点A是弧BC的中点,
∴∠ABC=∠ADB,
又∵∠BAE=∠BAE,
∴△ABE∽△ABD.(3分)
(2)解:∵△ABE∽△ADB,
∴AB2=2×6=12,
∴AB=2 ,
,
在Rt△ADB中,tan∠ADB= .(3分)
.(3分)
(3)解:连接CD,则∠BCD=90°;
由(2)得:∠ADB=∠EDC=30°,∠CED=60°;
已知DE=4,则CD=2 ;
;
∵S△BDF= ×BF×2
×BF×2 =8
=8 ,即BF=8;
,即BF=8;
易得∠EBD=∠EDB=30°,即BE=DE=4,
∴EF=DE=4,又∠CED=60°,
∴△DEF是正三角形,
故∠EDF=60°.(2分)
点评:此题主要考查了相似三角形的判定和性质、圆周角定理、圆心角、弧的关系、等边三角形的判定和性质等知识,难度适中.
(2)由(1)的相似三角形所得比例线段,可求得AB的长,进而可在Rt△ABD中,求得∠ABD的正切值.
(3)连接CD,由(2)知∠ADB=30°,那么∠CDE=30°,∠CED=60°,由DE的长即可得到CD的值,进而可由△BDF的面积求得BF的长,进而可求得EF=ED=4,由此可证得△EDF是正三角形,即可得∠EDF的度数.
解答:(1)证明:∵点A是弧BC的中点,
∴∠ABC=∠ADB,
又∵∠BAE=∠BAE,
∴△ABE∽△ABD.(3分)
(2)解:∵△ABE∽△ADB,
∴AB2=2×6=12,
∴AB=2
 ,
,在Rt△ADB中,tan∠ADB=
 .(3分)
.(3分)(3)解:连接CD,则∠BCD=90°;
由(2)得:∠ADB=∠EDC=30°,∠CED=60°;

已知DE=4,则CD=2
 ;
;∵S△BDF=
 ×BF×2
×BF×2 =8
=8 ,即BF=8;
,即BF=8;易得∠EBD=∠EDB=30°,即BE=DE=4,
∴EF=DE=4,又∠CED=60°,
∴△DEF是正三角形,
故∠EDF=60°.(2分)
点评:此题主要考查了相似三角形的判定和性质、圆周角定理、圆心角、弧的关系、等边三角形的判定和性质等知识,难度适中.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )
10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )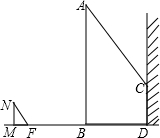 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
