Question

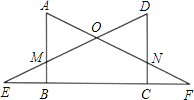
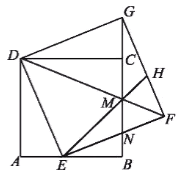
【题目】如图，在正方形ABCD中，点E是AB边上的一点，以DE为边作正方形DEFG，DF与BC交于点M，延长EM交GF于点H，EF与GB交于点N，连接CG.

（1）求证：CD⊥CG；

（2）若tan∠MEN=，求的值；

（3）已知正方形ABCD的边长为1，点E在运动过程中，EM的长能否为？请说明理由.

Answer 1

【答案】（1）见解析；（2）；（3）EM长不可能为.理由见解析.

【解析】

（1）由正方形的性质得出∠A=∠ADC=∠EDG=90°，AD=CD，DE=DG，即∠ADE=∠CDG，由SAS证明△ADE≌△CDG得出∠A=∠DCG=90°，即可得出结论；
（2）先证明△EDM≌△GDM，得出∠DME=∠NMF，，再证明△DME∽△FMN，得出，，在Rt△EFH中，tan∠HEF=，所以；

（3）假设EM= ，先判断出点G在BC的延长线上，同（2）的方法得，EM=GM=，得出GM=,再判断出BM＜，得出CM＞，进而得出CM＞GM，即可得出结论．

（1）证明：∵四边形ABCD和四边形DEFG是正方形，
∴∠A=∠ADC=∠EDG=90°，AD=CD，DE=DG，
∴∠ADE=∠CDG，
在△ADE和△CDG中，

∴△ADE≌△CDG（SAS），
∴∠A=∠DCG=90°，
∴CD⊥CG；

（2）解：

∵CD⊥CG，DC⊥BC，

∴G、C、M三点共线

∵四边形DEFG是正方形，

∴DG=DE，∠EDM=∠GDM=45°，

又∵DM=DM

∴△EDM≌△GDM，

∴∠DME=∠DMG

又∠DMG=∠NMF，

∴∠DME=∠NMF，

又∵∠EDM=∠NFM=45°

∴△DME∽△FMN，

∴

又∵DE∥HF，

∴，

又∵ED=EF，

∴

在Rt△EFH中，tan∠HEF=，

∴

（3）EM的长不可能为。

理由：假设EM的长为，

∵点E是AB边上一点，且∠EDG=∠ADC=90°，
∴点G在BC的延长线上，
同（2）的方法得，EM=GM=，

∴GM=，

在Rt△BEM中，EM是斜边，
∴BM＜

∵正方形ABCD的边长为1，
∴BC=1，
∴CM＞

∴CM＞GM，
∴点G在正方形ABCD的边BC上，与“点G在BC的延长线上”相矛盾，
∴假设错误，
即：EM的长不可能为