题目内容
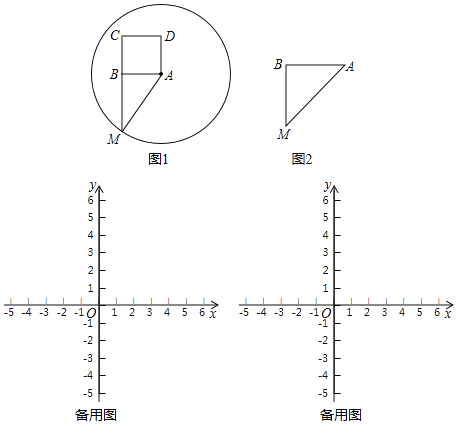
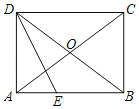
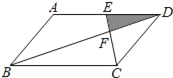
【题目】如图,在![]() 中,
中, ![]() .在同一平面内,
.在同一平面内,![]() 内部一点
内部一点![]() 到
到![]() 的距离都等于
的距离都等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() .
.
(1)直接写出![]() 的值;
的值;
(2)连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
①求证:![]() ;
;
②求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
【答案】(1)![]() ;(2)①见解析;②直线
;(2)①见解析;②直线![]() 与图形
与图形![]() 的公共点个数为1
的公共点个数为1
【解析】
(1)连接OA,OB,OC,推出∠A=90°,再根据S△ABC=S△AOB+S△BOC+S△AOC列式求解即可;
(2)根据题意得出OB平分∠ABC,即![]() ,再根据
,再根据![]() ,即可证明
,即可证明![]() ;
;
(3)设![]() 与
与![]() 的切点为
的切点为![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,证明
,证明![]() 即可得出答案.
即可得出答案.
解:(1)连接OA,OB,OC,
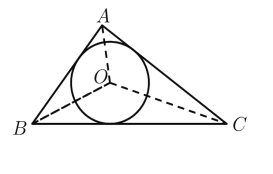
∵AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∴S△ABC=![]() ABAC=
ABAC=![]() ×3×4=6,
×3×4=6,
∵S△ABC=S△AOB+S△BOC+S△AOC
=![]() (AB+AC+BC)×a
(AB+AC+BC)×a
=![]() (3+4+5)×a
(3+4+5)×a
∴![]() ×12a=6
×12a=6
∴a=1;
(2)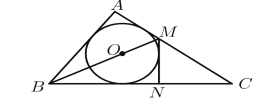
①由题意可知图形![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,![]() 与
与![]() 相切,
相切,
∵点O到AB、BC的距离为1,
∴OB平分∠ABC,
∴![]() ,
,
∵![]() ,
,
∴∠A=90°,
∵![]() ,
,
∴![]() ,
,
∴∠BMA=90°-∠ABM,
∠BMN=90°-∠NBM,
∴![]() ;
;
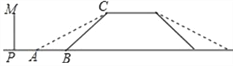
②如图,设![]() 与
与![]() 的切点为
的切点为![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,
,
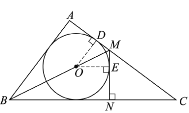
∵![]() ,OE⊥MN,
,OE⊥MN,
∴∠ODM=∠OEM,
由①可知∠BMA=∠BMN,
又∵OM=OM,
∴△ODM≌△OEM,
∴![]() ,
,
∴![]() 为
为![]() 的半径,
的半径,
∴![]() 为
为![]() 的切线,
的切线,
∴直线![]() 与图形
与图形![]() 的公共点个数为1.
的公共点个数为1.

练习册系列答案
相关题目