题目内容
 直角梯形ABCD中,AD∥BC,∠A=90°,AD=1,BC=
直角梯形ABCD中,AD∥BC,∠A=90°,AD=1,BC= ,点E是一腰CD的中点,BE的延长线与AD的延长线相交于点F.
,点E是一腰CD的中点,BE的延长线与AD的延长线相交于点F.
(1)求证:DF=CB;
(2)连接BD、CF,当AB=________时,四边形BCFD是菱形?请说明理由.
(1)证明:∵AD∥BC,
∴∠DFE=∠CBE,
又∵∠DEF=∠CEB,DE=CE,
∴△DFE≌△CBE(AAS),
∴DF=CB.
(2)解:当AB=2时,四边形BCFD是菱形,
理由如下:由(1)知:DF=BC,DF∥BC,
∴四边形BCFD是平行四边形,
∵∠A=90°,AD=1,
∴当AB=2时,BD= =
= =BC,
=BC,
∴?BCFD是菱形.
故答案为:2.
分析:(1)根据平行线的性质得出∠DFE=∠CBE,根据AAS推出△DFE≌△CBE即可;
(2)根据平行四边形的判定得出平行四边形,根据勾股定理求出BD=BC即可.
点评:本题主要考查对直角梯形的性质,平行线的性质,勾股定理,菱形的判定,平行四边形的判定等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.
∴∠DFE=∠CBE,
又∵∠DEF=∠CEB,DE=CE,
∴△DFE≌△CBE(AAS),
∴DF=CB.
(2)解:当AB=2时,四边形BCFD是菱形,
理由如下:由(1)知:DF=BC,DF∥BC,
∴四边形BCFD是平行四边形,
∵∠A=90°,AD=1,
∴当AB=2时,BD=
 =
= =BC,
=BC,∴?BCFD是菱形.
故答案为:2.
分析:(1)根据平行线的性质得出∠DFE=∠CBE,根据AAS推出△DFE≌△CBE即可;
(2)根据平行四边形的判定得出平行四边形,根据勾股定理求出BD=BC即可.
点评:本题主要考查对直角梯形的性质,平行线的性质,勾股定理,菱形的判定,平行四边形的判定等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
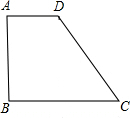 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为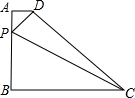 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为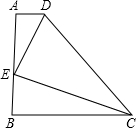 下结论:
下结论: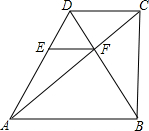 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.