题目内容
如图,在直角三角形ABC中,∠AC B=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
B=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
(1)CD的长;
(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(3)作出△BCD的边BC边上的高DF,当BD=11cm 时,求DF的长。
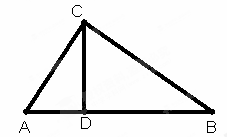
解:(1)在直角三角形ABC中,∠ACB=90° BC=12cm AC=5cm
∴△ABD的面积为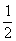 BC·AC=
BC·AC=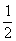 ×12×5=30cm2
×12×5=30cm2
∵CD是AB边上的高 AB=13cm
∴△ABD的面积又等于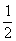 AB·CD=
AB·CD=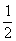 ×13CD=
×13CD=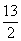 CD
CD
∴30=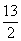 CD ∴CD=
CD ∴CD=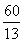 cm
cm
(2)作图略
∵BE是边AC的中线 AC=5cm ∴CE=2.5cm
∵∠ACB=90° ∴△BEC的面积=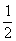 CE·BC=15cm2
CE·BC=15cm2
∴△ABE的面积=△ABC的面积-△BEC的面积
=30-15=15cm2
(3)作图略
∵DF是△A BC 的BC边上的高 CD是AB边上的高,
BC 的BC边上的高 CD是AB边上的高,
BD=11cm CD=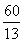 cm
cm
∴△CDB的面积=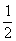 CD·BD=
CD·BD=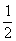 BC·DF
BC·DF
即
 ×11=
×11= ×12×DF
×12×DF
∴DF=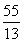 cm
cm

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

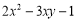 是二次三项式
是二次三项式  不是单项式
不是单项式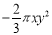 的系数是
的系数是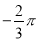
 的次数是6
的次数是6

 是( )
是( )