题目内容
如图，屋架的横梁BC=10m，中柱AD=| 5 |
| 3 |
| 3 |
（1）求支柱EF的长度．
（2）求斜柱DF的长度．
分析：（1）根据AD∥EF得到三角形相似，利用相似三角形对应边的比相等列出比例式求解即可；
（2）利用勾股定理求解即可．
（2）利用勾股定理求解即可．
解答：解：（1）∵EF⊥BC，AD⊥BC
∴△BEF∽△BDA
∴
=
∵BC=10m，AD=
m，BE=3m．
∴
=
解得：EF=
；
（2）在Rt△FED中，EF=
，DE=BD-BE=5-3=2m，
∴DF=
=
∴△BEF∽△BDA
∴
| EF |
| AD |
| BE |
| BD |
∵BC=10m，AD=
| 5 |
| 3 |
| 3 |
∴
| EF | ||||
|
| 3 |
| 5 |
解得：EF=
| 3 |
（2）在Rt△FED中，EF=
| 3 |
∴DF=
22+(
|
| 7 |
点评：本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形．
练习册系列答案
阅读快车系列答案
相关题目
18、如图是屋架设计图的一部分，立柱BC垂直于横梁AC，BC=4米，∠A=30°，则斜梁AB=
如图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=8m，∠A=30°，则DE=
如图是屋架设计图的一部分，其中∠A=30°，点D是斜梁AB的中点，BC、DE垂直于横梁AC，AB=16m，则DE的长为（ ）| A、8m | B、4m | C、2m | D、6m |
如图，屋架的横梁BC=10m，中柱AD=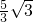
m，EF⊥BC，BE=3m．