Question

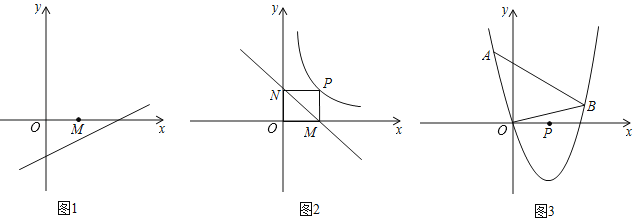
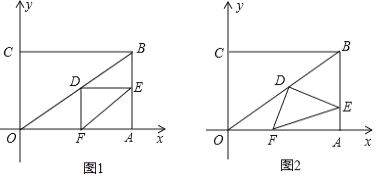
【题目】在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连接OB，点D为OB的中点，点E是线段AB上的动点，连接DE，作DF⊥DE，交OA于点F，连接EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．

（1）如图1，当t=3时，求DF的长．

（2）如图2，当点E在线段AB上移动的过程中，的大小是否发生变化？如果变化，请说明理由；如果不变，请求出的值．

（3）连接AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．

Answer 1

【答案】（1）（2）不变，（3）t=或

【解析】

（1）当t=3时，点E为AB的中点，由三角形中位线定理得出DE∥OA，DE=OA=4，再由矩形的性质证出DE⊥AB，得出∠OAB=∠DEA=90°，证出四边形DFAE是矩形，得出DF=AE=3即可；

（2）作DM⊥OA于M，DN⊥AB于N，证明四边形DMAN是矩形，得出∠MDN=90°，DM∥AB，DN∥OA，由平行线得出比例式，，由三角形中位线定理得出DM=AB=3，DN=OA=4，证明△DMF∽△DNE，得出的值；

（3）作作DM⊥OA于M，DN⊥AB于N，若AD将△DEF的面积分成1：2的两部分，设AD交EF于点G，则点G为EF的三等分点；

①当点E到达中点之前时，NE=3-t，由△DMF∽△DNE得：MF=（3-t），求出AF=4+MF=，得出G（，），求出直线AD的解析式为y=，把G（，）代入即可求出t的值；

②当点E越过中点之后，NE=t-3，由△DMF∽△DNE得：MF=，求出AF=4-MF=，得出G（，），代入直线AD的解析式y=求出t的值即可．

解：（1）当t=3时，点E为AB的中点，

∵A（8，0），C（0，6），

∴OA=8，OC=6，

∵点D为OB的中点，

∴DE∥OA，DE=OA=4，

∵四边形OABC是矩形，

∴OA⊥AB，

∴DE⊥AB，

∴∠OAB=∠DEA=90°，

又∵DF⊥DE，

∴∠EDF=90°，

∴四边形DFAE是矩形，

∴DF=AE=3；

（2）的大小不变；

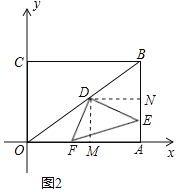
理由：如图2所示：作DM⊥OA于M，DN⊥AB于N，

∵四边形OABC是矩形，

∴OA⊥AB，

∴四边形DMAN是矩形，

∴∠MDN=90°，DM∥AB，DN∥OA，

∴，，

∵点D为OB的中点，

∴M、N分别是OA、AB的中点，

∴DM=AB=3，DN=OA=4，

∵∠EDF=90°，

∴∠FDM=∠EDN，

又∵∠DMF=∠DNE=90°，

∴△DMF∽△DNE，

∴．

（3）作DM⊥OA于M，DN⊥AB于N，

若AD将△DEF的面积分成1：2的两部分，

设AD交EF于点G，则点G为EF的三等分点；

①当点E到达中点之前时，如图3所示，NE=3-t，

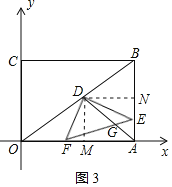
由△DMF∽△DNE得：MF=，

∴，

∵点G为EF的三等分点，

∴G（，），

设直线AD的解析式为y=kx+b，

把A（8，0），D（4，3）代入得：，

解得：，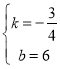

∴直线AD的解析式为：，

把点G（，）代入得：；

②当点E越过中点之后，如图4所示，NE=t-3，

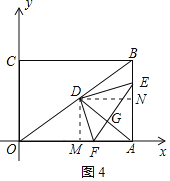
由△DMF∽△DNE得：MF=，

∴，

∵点G为EF的三等分点，

∴G（，），

把点G代入直线AD的解析式，

解得：；

综合上述，当AD将△DEF分成的两部分的面积之比为1：2时，的值为或.