题目内容
1.将边长为1的正方形纸片按图1进行二等分分割,其阴影图形面积为S1,继续将图2剩下空白部分二等分分割的图形面积为S2,…,按此方法如图3第n次分割后得到的图形面积为Sn,求S1+S2+S3+…+Sn=1-$\frac{1}{{2}^{n}}$.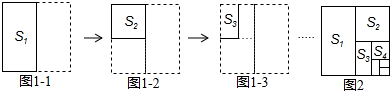
分析 先分别计算S1,S1+S2,S1+S2+S3,再根据计算结果找出规律即可求得S1+S2+S3+…+Sn.
解答 解:S1=$\frac{1}{2}$=1-$\frac{1}{2}$
S1+S2=$\frac{1}{2}$+$\frac{1}{4}$=1-$\frac{1}{4}$=1-$\frac{1}{{2}^{2}}$
S1+S2+S3=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$=1-$\frac{1}{8}$=1-$\frac{1}{{2}^{3}}$
…
S1+S2+S3+…+Sn=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$
故答案为:1-$\frac{1}{{2}^{n}}$
点评 本题主要考查了列代数式,解决问题的关键是根据计算S1,S1+S2,S1+S2+S3所得的结果找出规律.探寻规律时要认真观察、仔细思考,善用联想来解决这类问题.

练习册系列答案
相关题目
10.等腰三角形的顶角为100°,则它的一个底角是( )
| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
11. 如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
 如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 4$\sqrt{2}$ |
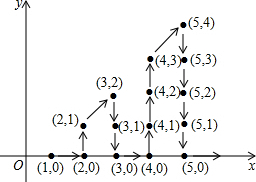 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63.
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63.