题目内容
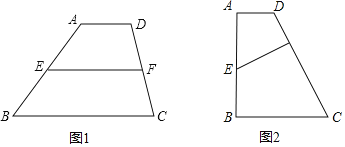
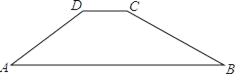
【题目】如图所示，某水库大坝的横断面是梯形ABCD，坝顶宽CD=3m，斜坡AD=8m，斜坡BC的坡度i=1：3，B，C间的水平距离为12m，则斜坡AD的坡角∠A=_____，坝底宽AB=______m．
【答案】30° （15+4
）．
【解析】
过D点作DE⊥AB于点E，过C点作CF⊥AB于点F，得到两个直角三角形和一个矩形．在Rt△BCF、Rt△AED中已知坡度和一边，或两边的比，满足解直角三角形的条件，可求出CF、DE的长度，继而根据AD=8m，可求得∠A的度数，然后解直角三角形可求得AE的长，继而也可求得AB的长度．
过D点作DE⊥AB于点E，过C点作CF⊥AB于点F，则四边形CDEF是矩形，∴CD=FE=3m，DE=CF．
∵斜坡BC的坡度i=1：3，BF=12m，∴CF：BF=1：3，则CF=
×12=4m．
∵AD=8m，∴sinA=DE：AD=4：8=1：2，∴∠A=30°，AE=ADcos30°=4（m），∴AB=AE+EF+FB=4+3+12=15+4．
故答案为：30°，（15+4）．
练习册系列答案
相关题目
