Question

如图，⊙O中弦AB等于半径R，则这条弦所对的圆心角是

60°

，圆周角是

30°或150°

．

Answer 1

分析：先作出弦AB所对的圆心角与圆周角，再根据圆周角定理可得到∠APB=30°，然后根据圆内接四边形的性质得到∠AP′B=150°．

解答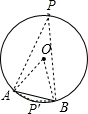：解：连结OA、OB，∠APB和∠AP′B为弦AB所对的圆周角，如图，
∵弦AB等于半径R，
∴△OAB为等边三角形，
∴∠AOB=60°，
∴∠APB=

1

2

∠AOB=30°，
∴∠AP′B=180°-∠APB=150°，
即这条弦所对的圆心角是60°，圆周角是30°或150°．
故答案为60°；是30°或150°．

点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等边三角形的判定与性质以及圆内接四边形的性质．