题目内容
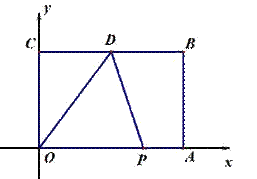
已知:如图,平面直角坐标系中,矩形OABC的顶点A(6,0)、B(6,4),D是BC的中点.动点P从O点出发,以每秒1个单位的速度,沿着OA、AB、BD运动.设P点运动的时间为t秒(0<t<13).
(1) 写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(2) 当点P在OA上运动时,连结CP.问:是否存在某一时刻t,当CP绕点P旋转时,点C能恰好落到A B的中点M处?若存在,请求出t的值并判断此时△CPM的形状;若不存在,请说明理由;
B的中点M处?若存在,请求出t的值并判断此时△CPM的形状;若不存在,请说明理由;
(3)当点P在AB上运动时,试探索当PO+PD的长最短时的直线PD的表达式。

 备用图
备用图
分值分配,6+3+2


(3) y=-

练习册系列答案
相关题目
 1.5cm,则BC=__________cm.
1.5cm,则BC=__________cm.
 r;③
r;③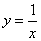 ;④
;④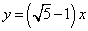 ;⑤y=-(a+x)(a是常数);
;⑤y=-(a+x)(a是常数);
 AB.
AB.
 比例函数
比例函数 的图像上,则代数式ab的值为( )
的图像上,则代数式ab的值为( )
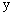 轴交于点C(0,3),与
轴交于点C(0,3),与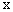 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。