题目内容
如图,已知长方形ABCO中,边AB=12,BC=6,以点O为原点,OA、OC所在的直线为y轴和x轴建 立直角坐标系.
立直角坐标系.
(1)若点A的坐标为(0,6),则B、C两点的坐标分别为
(2)若在y轴上存在一点M,使△ACM的面积是长方形ABCO面积的
,则点M的坐标为
(3)若点P从C点出发,以2单位/秒的速度向CO方向移动(不超过点O),点Q从原点O出发,以1单位/秒的速度向OA方向移动(不超过点A);P、Q两点同时出发,设移动时间为t秒,则:
①AQ=
②在它们移动过程中,四边形OPBQ的面积是否发生变化?若不变,求其值;若变化,求其变化范围.
 立直角坐标系.
立直角坐标系.(1)若点A的坐标为(0,6),则B、C两点的坐标分别为
(12,6)
(12,6)
和(12,0)
(12,0)
.(2)若在y轴上存在一点M,使△ACM的面积是长方形ABCO面积的
| 1 | 3 |
(0,2)或(0,10)
(0,2)或(0,10)
.(3)若点P从C点出发,以2单位/秒的速度向CO方向移动(不超过点O),点Q从原点O出发,以1单位/秒的速度向OA方向移动(不超过点A);P、Q两点同时出发,设移动时间为t秒,则:
①AQ=
6-t
6-t
,CP=2t
2t
(用含t的式子表示);②在它们移动过程中,四边形OPBQ的面积是否发生变化?若不变,求其值;若变化,求其变化范围.
分析:(1)根据坐标系中点的表示法即可得到;
(2)首先求得长方形ABCO的面积,设AM=x,根据三角形的面积公式即可求得AM的长,则M的坐标即可求得;
(3)①根据距离=速度×时间即可表示;
②利用t表示出△ABQ和△BCP的面积,根据S四边形OPBQ=S长方形ABCO-S△ABQ-S△BCP即可求解,根据结果即可判断.
(2)首先求得长方形ABCO的面积,设AM=x,根据三角形的面积公式即可求得AM的长,则M的坐标即可求得;
(3)①根据距离=速度×时间即可表示;
②利用t表示出△ABQ和△BCP的面积,根据S四边形OPBQ=S长方形ABCO-S△ABQ-S△BCP即可求解,根据结果即可判断.
解答:解:(1)∵长方形ABCO中,OC=AB=6,AB=12,BC=6,
∴B的坐标是(12,6),C的坐标是(6,0);
(2)长方形ABCO的面积是:AB•BC=12×6=72,
设AM=x,则
x×12=
×72,
解得:x=4,
则M的坐标是(0,2)或(0,10);
(3)①OQ=t,CP=2t,则AQ=6-t;
②S△ABQ=
AB•AQ=
×12(6-t)=36-6t,
S△BCP=
PC•BC=
×2t×6=6t,
则S四边形OPBQ=S长方形ABCO-S△ABQ-S△BCP=72-(36-6t)-6t=36.
故四边形OPBQ的面积不随t的增大而变化.
∴B的坐标是(12,6),C的坐标是(6,0);
(2)长方形ABCO的面积是:AB•BC=12×6=72,
设AM=x,则
| 1 |
| 2 |
| 1 |
| 3 |
解得:x=4,
则M的坐标是(0,2)或(0,10);
(3)①OQ=t,CP=2t,则AQ=6-t;
②S△ABQ=
| 1 |
| 2 |
| 1 |
| 2 |
S△BCP=
| 1 |
| 2 |
| 1 |
| 2 |
则S四边形OPBQ=S长方形ABCO-S△ABQ-S△BCP=72-(36-6t)-6t=36.
故四边形OPBQ的面积不随t的增大而变化.
点评:本题考查了点的坐标的表示,长方形的性质以及三角形的面积公式,正确表示四边形OPBQ的面积是关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 48、如图,已知长方形的台球桌台ABCD,有黑、白两球分别位于M、N两点的位置上,试问:怎样撞击白球N,才能让白球先撞台边AB,反弹后再击中黑球M.
48、如图,已知长方形的台球桌台ABCD,有黑、白两球分别位于M、N两点的位置上,试问:怎样撞击白球N,才能让白球先撞台边AB,反弹后再击中黑球M. 8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( )
8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( ) 如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则EF=
如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则EF=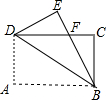 如图,已知长方形ABCD沿着直线BD折叠,使点A落在点E处,EB交DC于F,BC=3,AB=4,则点F到直线DB的距离为
如图,已知长方形ABCD沿着直线BD折叠,使点A落在点E处,EB交DC于F,BC=3,AB=4,则点F到直线DB的距离为 如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互