Question

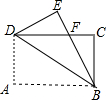如图，已知长方形ABCD沿着直线BD折叠，使点A落在点E处，EB交DC于F，BC=3，AB=4，则点F到直线DB的距离为

15

8

．

Answer 1

分析：根据折叠的性质以及矩形的性质易证△DFB是等腰三角形，则利用勾股定理即可求得FC的长，则△BCF的面积可以求得，进而求得△BCD的面积，根据三角形的面积公式即可求得FG的长．

解答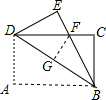：解：作FG⊥BD于点G．
∵矩形纸片沿对角线BD翻折，点A落在点E处
∴∠FBD=∠ABD，△DEB≌△BCD，
∴∠DBE=∠CDB，
∴DF=FB，
∴△DFB是等腰三角形．
设FC=x，则BF=DF=4-x，
在直角△BCF中，BF²=CF²+BC²，即（4-x）²=x²+3²，
解得：x=

7

8

，
则S_△BCF=

1

2

BC•CF=

1

2

×3×

7

8

=

21

16

．
∵S_△BCD=

1

2

BC•CD=

1

2

×3×4=6，
∴S_△BDF=S_△BCD-S_△BCF=6-

21

16

=

75

16

，
在直角△BCD中，BD=

BC2+BD2

=

32+42

=5，
又∵S_△BDF=

1

2

BD•FG，
∴FG=

2× 75 16

5

=

15

8

．
故答案是：

15

8

．

点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．