题目内容
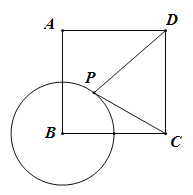
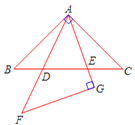
【题目】已知：如图，在长方形
中，
，动点
从点
出发，以每秒
的速度沿
方向向点
运动，动点
从点出发，以每秒
的速度沿
向点运动，
同时出发，当点停止运动时，点也随之停止，设点运动的时间为
秒．请回答下列问题：
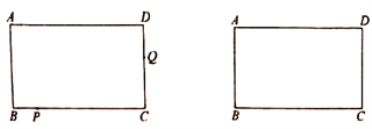
（1）请用含的式子表达
的面积
，并直接写出的取值范围．
（2）是否存在某个值，使得
和
全等？若存在，请求出所有满足条件的值；若不存在，请说明理由．
【答案】（1）
（0<t≤1.5），
（1.5<t≤4），
（4<t<5）；（2）当t=3时，△ABP和△CDQ全等．
【解析】
（1）分别讨论①当Q在CD上时，②当Q在DA上时， ③当Q在AB上时，表示出CQ，BP求出面积即可；
（2）分别讨论①当Q在CD上时，②当Q在AD上时，③当Q在AB上时，求出△ABP和△CDQ全等时的t值.
解：（1）①当Q在CD上时，
如图，由题意得CQ=2t，BP=t
∴CP=5t（0<t≤1.5）
②当Q在DA上时，（1.5<t≤4）
③当Q在AB上时，由题意得BQ=112t（4<t<5）
（2）①当Q在CD上时，不存在t使△ABP和△CDQ全等
②当Q在AD上时，
如图，由题意得DQ=2t3
要使△ABP≌△CDQ，则需BP=DQ
∵DQ=2t3，BP=t
∴t=2t3，t=3
即当t=3时，△ABP≌△CDQ．
③当Q在AB上时，不存在t使△ABP和△CDQ全等
综上所述，当t=3时，△ABP和△CDQ全等．
练习册系列答案
相关题目
