题目内容
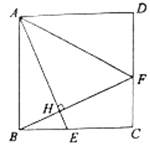
如图,已知抛物线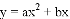 与
与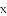
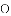
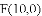

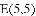
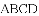
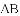
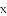
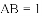
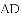
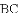
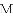
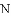
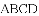
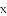
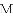
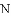

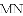
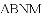
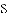
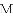
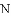

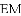
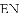
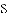
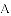
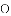
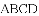
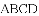
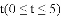
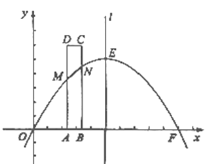
(1)求出这条抛物线的表达式;
(2)当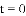
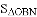 的值;
的值;
(3)当矩形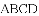
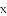
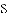
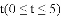

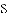
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目


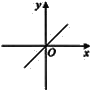 B.
B. 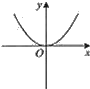 C.
C. 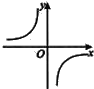 D.
D. 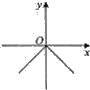
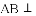
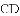
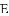
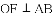
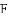
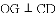
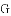
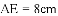
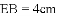
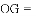
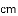
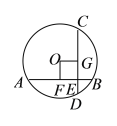
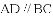
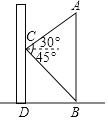
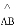 与
与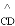 的数量关系是( )
的数量关系是( )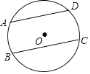
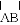 =
=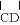 B.
B. 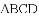
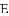
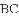
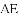
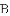
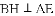
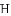
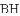
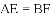
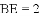
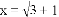 ,求代数式
,求代数式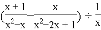 的值
的值