Question

如图：△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB与AC、AE分别交于点O、E，连接EC.

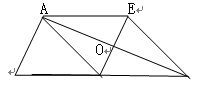
1.求证：AD=EC；（4分）

2.当∠BAC=90º时,求证:四边形ADCE是菱形；（3分）

3.在(2)的条件下,若AB=AO,且OD=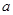,求菱形ADCE的周长.（5分）

 

Answer 1

 

1.∵AE∥BC，DE∥AB   ∴四边形ABDE是平行四边形（1分）

∴AE=BD  ∵D是BC中点 ∴DC=DB（2分）

∴AE=DC ，AE∥DC ∴四边形ADCE是平行四边形（3分）

∴AD=EC（4分）

2.当∠BAC=90º时，AD是Rt△ABC斜边上的中线，（5分）

∴AD=（6分）

∴四边形ADCE是菱形（有一组邻边相等的平行四边形是菱形）（7分）

3.∵ADCE是菱形  ∴对角线AC⊥DE且O是DE中点（8分）

∵ABDE是平行四边形 ∴AB=DE 又已知AB=AO

∴AO=DE=2DO=2 （10分）

在Rt△AOD中，可求出AD=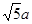 （11分）

∴菱形ADCE的周长为4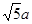（12分）

解析:（1）先证四边形ABDE是平行四边形，再证四边形ADCE是平行四边形，即得AD=CE；

（2）由∠BAC=90°，AD上斜边BC上的中线，即得AD=BD=CD，证得四边形ADCE是平行四边形，即证；

（3）利用菱形和平行四边形的性质求出菱形一边的长度，然后再求出它的周长。