题目内容
某人只带了2元和5元两种纸币(两种纸币都足够多),他要买一件27元的商品,而商店不给找钱,要他恰好付27元,他付钱方式的种数是
- A.1
- B.2
- C.3
- D.4
C
分析:设2元的用x枚,5元的用y枚,根据总价为27元建立方程,再根据x,y的取值范围和本题的实际求出符合条件的付钱方式即可.
解答:设2元的用x枚,5元的用y枚,由题意,得
2x+5y=27,
x= .
.
∵x≥0,y≥0为整数,
∴ ≥0,
≥0,
∴0≤y≤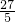 ,
,
∴y=0,1,2,3,4,5
当y=0时,
x= 舍去,
舍去,
当y=1时,
x=11,
当y=2时,
x= 舍去,
舍去,
当y=3时,
x=6,
当y=4时,
x= 舍去,
舍去,
当y=5时,
x=1,
则共有3种付款方式.
故选C.
点评:本题考查了二元一次方程的应用,解答时根据题目的隐含条件x、y为大于等于0的整数求解是关键,用方程解答实际问题时需要注意所求的解要符合实际意义.
分析:设2元的用x枚,5元的用y枚,根据总价为27元建立方程,再根据x,y的取值范围和本题的实际求出符合条件的付钱方式即可.
解答:设2元的用x枚,5元的用y枚,由题意,得
2x+5y=27,
x=
 .
.∵x≥0,y≥0为整数,
∴
 ≥0,
≥0,∴0≤y≤
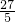 ,
,∴y=0,1,2,3,4,5
当y=0时,
x=
 舍去,
舍去,当y=1时,
x=11,
当y=2时,
x=
 舍去,
舍去,当y=3时,
x=6,
当y=4时,
x=
 舍去,
舍去,当y=5时,
x=1,
则共有3种付款方式.
故选C.
点评:本题考查了二元一次方程的应用,解答时根据题目的隐含条件x、y为大于等于0的整数求解是关键,用方程解答实际问题时需要注意所求的解要符合实际意义.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
某人只带了2元和5元两种货币,他要买一件27元的商品,而商店不给找钱,则此人的付款方式有( )
| A、1种 | B、2种 | C、3种 | D、4种 |