题目内容
Rt△ABC中,∠C=90°,若sinA和sinB是方程x2-| 2 |
分析:根据锐角三角函数关系式,得sin2A+sin2B=1;根据一元二次方程根与系数的关系,得sinA+sinB=
,sinA•sinB=-k,再进一步利用完全平方公式得到关于k的方程进行求解.
| 2 |
解答:解:∵sinA和sinB是方程x2-
x-k=0的两个根,
∴sinA+sinB=
,sinA•sinB=-k,
∵Rt△ABC中,∠C=90°,
∴sin2A+sin2B=1,
∴2+2k=1,
解得,k=-
.
故答案为:-
.
| 2 |
∴sinA+sinB=
| 2 |
∵Rt△ABC中,∠C=90°,
∴sin2A+sin2B=1,
∴2+2k=1,
解得,k=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:此题综合考查了一元二次方程根与系数的关系以及锐角三角函数关系式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
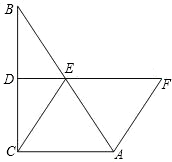 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=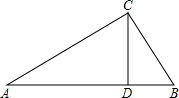 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=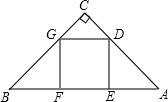 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为